#задача

Страсти по признаку вписанного четырёхугольника. От классики через экстремальность к новаторству или как же его всё-таки доказать.
https://telegra.ph/Kazhushchayasya-prostota-i-realnaya-slozhnost-obratnyh-zadach-03-24
#статья

на картинке — теорема Морли (Морлея) о том, что трисектрисы углов любого треугольника пересекаются в вершинах правильного треугольника

у нее есть разные доказательства — не очень простые, но интересные

а вот 3 достаточно коротких доказательства теоремы Морли в Кванте 2009-05, в т.ч. доказательство Конвея

Окружность девяти точек

Геогебра позволяет доказывать без слов довольно сложные теоремы.
Вот пример – теорема об окружности девяти точек (идея доказательства взята у Jonaki Ghosh). Даём формулировку теоремы, а дальше показываем чертёж, на котором постепенно появляются новые элементы.

К каждому шагу задайте три вопроса:
– Что произошло?
– Что мы заметили?
– Почему это так?
И школьники 8-9 класса сами расскажут доказательство.

Динамическая модель оказывается аналогом «листка с заданиями». Шаги построения соответствуют леммам – пунктам листочка, а точный чертёж заменяет явно сформулированные утверждения.

https://www.geogebra.org/m/pv7xqpwk

Другие примеры использования динамических моделей для решения геометрических задач можно найти в книге «Геометрия на подвижных чертежах» (https://biblio.mccme.ru/node/6426/shop).

Пусть «Математический вторник» на этой неделе начнётся в понедельник. Премьера-подарок сайта «Математические этюды» – сюжет «Сферы Данделена».

Два самых известных определения эллипса – через натянутую ниточку с концами в фокусах и как сечение конуса. Как они связаны? Откуда у сечения конуса берутся эти выделенные точки – фокусы? Почему у эллипса и гиперболы по два фокуса, а у параболы – один? В геометрическом определении параболы участвует директриса. А есть ли директриса у эллипса и, если да, то что это такое? Свести факты о кониках в единую картину и позволяют сферы (шары) Данделена.

Хм... вчерашний пост стал самым залайканным и перепостнутым в истории канала. А всего то и требовалось — сделать трехмесячный перерыв. Давайте разовьем успех!

Сравним задачи с питерской олимпиады и московской? Ниже задача, предложенная в восьмом классе под номером 4 на ММО этого года. Разница между ММО и СПбМО колоссальна, конечно. В восьмом классе СПбМО участвует около 100 школьников, в ММО — около 2500. В Питере олимпиада устная и состоит из 7 задач, а в Москве письменная и состоит из 6 задач. Но все же... набор идей, необходимых для решения приблизительно один и тот же.

№40. В правильном пятиугольнике ABCDE отмечена точка F — середина CD. Серединный перпендикуляр к AF пересекает CE в точке H. Докажите, что прямая AH перпендикулярна прямой CE.

Гифка по вторникам: лемма Архимеда

Я уже как-то писал, что мне очень нравятся геометрические задачи с польских олимпиад. На польской олимпиаде этого года прошел второй тур. Геометрия с этой олимпиады ниже.

№45. На стороне DC параллелограмма ABCD отмечена точка E такая, что углы ABD и EBC равны. Окружность с центром O проходит через точки D и E и касается прямой AD в точке D. Докажите, что точка O равноудалена от точек A и C.

Гифка по вторникам: теорема о бабочке.

Во второй день на EGMO геометрическая задача была первой.

№49. Пусть I — центр вписанной окружности треугольника ABC, a D — произвольная точка на стороне BC. Прямая, проходящая через D перпендикулярно BI, пересекает прямую CI в точке E, а прямая, проходящая через D перпендикулярно CI, пересекает прямую BI в точке F. Докажите, что точка, симметричная точке A относительно прямой EF, лежит на прямой BC.

Финал всеросса. Задача 10.1.

На стороне BC параллелограмма ABCD выбраны точки E и F так, что E лежит между B и F. O — центр параллелограмма. Оказалось, что прямые AE и DF касаются окружности, описанной около треугольника AOD. Докажите, что они касаются и окружности, описанной около треугольника EOF.

на страницу https://olympiads.mccme.ru/vmo/ добавлены задачи и решения всероссийской олимпиады по математике этого года (17-18 апреля)

Всероссийская олимпиада 2021. Второй день. Задача 9.6.

В неравнобедренном остроугольном треугольнике ABC с углом B равным 60° отмечены точки Торричелли T и пересечения медиан M. Прямая TM пересекает повторно окружность, описанную около треугольника ACT в точке K. Найдите TM/MK.

Прекрасный текст об уроке геометрии: https://m.facebook.com/story.php?story_fbid=10220226404114878&id=1370725427
Приведу его целиком:

Критическое мышление, гражданская позиция и геометрия

На последнем уроке геометрии в 7 классе говорили про геометрические места точек, строили с помощью циркуля и линейки, а потом анализировали, что же построили, и доказывали, то ли это самое, что хотели. Со всеми бывает.

В какой-то момент встал вопрос – всегда ли точка, равноудаленная от вершин треугольника, находится внутри треугольника.
У меня получилось так сильно поддержать первый ответ «Конечно», что весь класс с этим сразу согласился. Весь класс, кроме одного мальчика, который тихонечко начал рассматривать различные варианты и искать противоречие в наших рассуждениях.
Я занял позицию очень близко к нему – чтобы видеть, в какую сторону он движется. Но продолжал вместе с большинством семиклассников развивать доказательную базу под заведомо ложное утверждение. Почти сразу к поискам и размышлениям мальчика присоединилась девочка, усомнившаяся в мнении большинства.
В течение минуты у каждого из них родился контрпример ко всем нашим размышлениям. И они по одиночке стали пробовать его явить классу. А я продолжал с ними бороться, а не поддерживать – хотел увидеть, смогут ли они противостоять не только целому классу (большинство которого пыталась убедить их в том, что «снова они за свое», им больше всех надо и геометрия – не место для споров), но и учителю, с которым работают почти 3 года.

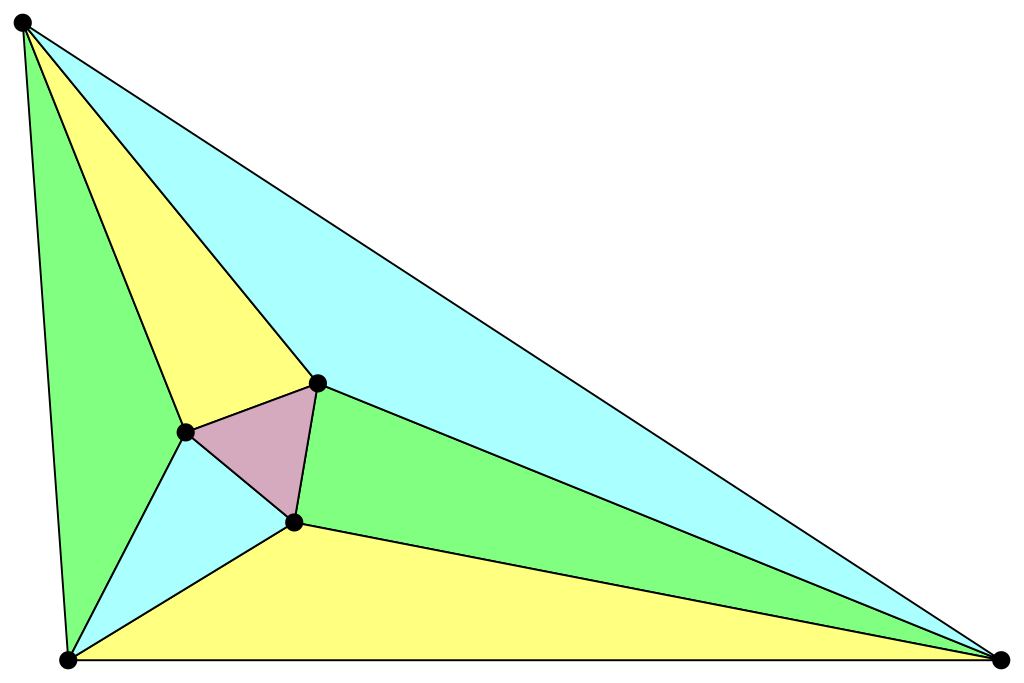
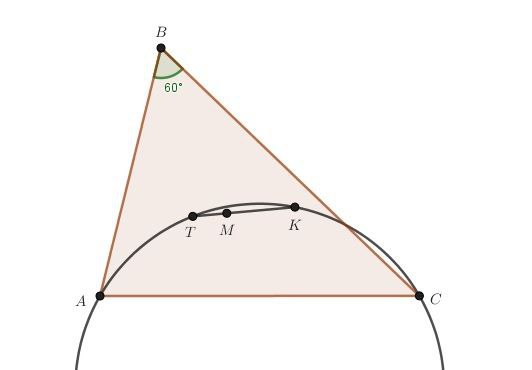
И они смогли! Мальчик вышел к доске (без разрешения, кстати), взял маркер и начертил тупоугольный треугольник. А потом построил точку пересечения серединных перпендикуляров, которая оказалась за границами треугольника (и это нормально).
Девушка в этот момент убедила двух соседей в том, что если взять три точки на окружности близко друг к другу и построить треугольник, то центр этой окружности будет находиться на равном расстоянии от вершин данного треугольника, но не внутри него. Мальчик сразу построил окружность вокруг собственного треугольника и подтвердил размышления девушки.
В этот момент весь класс понял, что версия мальчика с девочкой не только верная, но еще и доказанная. Случилась небольшая пауза, после которой почти все одноклассники проявили уважение к позиции несогласных и ищущих. Справедливость восторжествовала, награда нашла героев.

Но мне этого показалось мало.
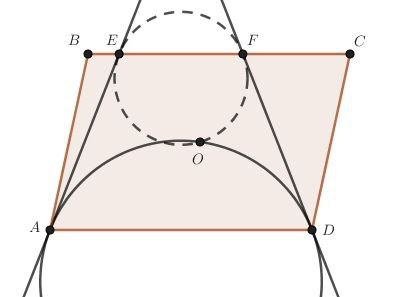
Предложил ребятам подумать про ситуацию с четырьмя точками – всегда ли существует точка на плоскости, равноудаленная от вершин произвольного четырехугольника. Оказалось, что это довольно трудно установить, т.к. точки могут быть где угодно..
На второй минуте размышлений у одного из учеников «родился» квадрат, в котором получилось найти такую точку. Сосед расширил эту идею до прямоугольников, и мы дружно перенесли все это на доску.
И в этот момент я внес в поле вторую провокацию: построил ромб и отметил точку пересечения его диагоналей, после чего отметил, что она делит каждую диагональ пополам. И назвал эту точку равноудаленной от вершин ромба.
Почти все семиклассники спокойно и размеренно стали перечерчивать примеры к себе в тетрадь. Кто-то дописывал что-то с предыдущего такта урока, кто-то на секунду отвлекся.
И только герой предыдущей ситуации крайне озадаченно смотрел на доску. Девушка-соседка быстро его поддержала – также повысила свою бдительность. После чего они снова стали робко молвить: «Юрий Анатольевич, у вас там ошибка»..  
И весь класс снова на них напал, не вникая в суть: снова вы за свое; если один раз получилось, теперь всегда так делать будете; не придирайтесь, мы же ничего решить не успеем сегодня…

Ребятам снова пришлось выйти к доске, показать ошибку, а потом представить доказательства того, что здравый смысл и внешний вид построенного значительно расходятся с тем, что говорит учитель.

Некоторое замешательство в головах и на лицах собравшихся.
Полная тишина. Шок.
Как можно было дважды за 15 минут наступить на одни и те же грабли?…
Что нас толкало атаковать «выделяющихся» и сомневающегося в разумности происходящего?..

После 20-секундной паузы торжественно пожал руки несогласным и ищущим, выразил всяческую поддержку.
Потом говорили про критическое мышление - что это, почему хорошо и как применять.  

Кто бы мог подумать, что геометрия – прекрасное место для развития гражданской позиции…