Вот прошлогодний: https://zen.yandex.ru/media/pouchi/dodekaedr--kalendar-2020-5e050ba20be00a00b07e2ace

Вдруг он вам приятней окажется.

#задача
Говорят, самая красивая задача 2020

пара задач из статьи И.Сиротовского и А.Шкловера в январском Квантике

Вот так сейчас выглядит Перге — родина Аполлония Пергского.

Все эти коллонны появились там лет на 300 позже Аполлония, а раскопаны в последние 50-80 лет (и много всего еще не раскопано).

Аполлоний был учеником Евклида, описал конические сечения, вернулся на родину и основал там учебный центр и библиотеку.

Пользуясь случаем напомним задачу Аполлония: построить окружность, касающуюся трех данных окружностей.

Мы писали про живые чертежи с упрощениями задачи Аполлония:
https://t.me/geometrykanal/665
https://t.me/geometrykanal/698

А вот видеозапись семинара, где Алексей Сгибнев рассказывал про компьютерный практикум вокруг задачи Аполлония:
https://youtu.be/dCeZJjeVfQo
Листок с задачами практикума:
https://t.me/geometrykanal/921

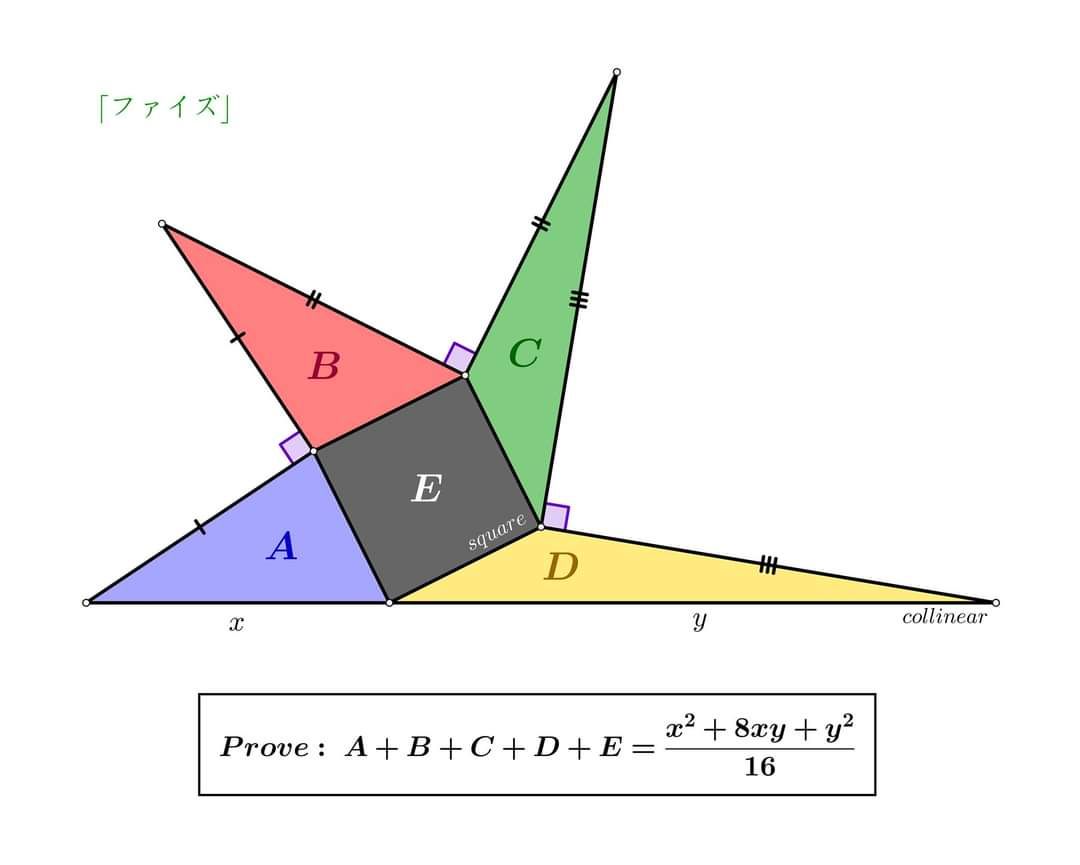
Теорема Пифагора: доказательство Евклида

Ввиду важности темы, элегантности и элементарности доказательства, а так же уникальной технической реализации, «windmill proof» теоремы Пифагора обрело свою отдельную страницу https://etudes.ru/etudes/pythagorean-theorem-windmill-proof/ .

Три вариации этого красивого доказательства теперь снабжены не менее красивой анимацией, реализованной по технологии анимированных SVG-файлов. И это новый формат точных математических чертежей: каждое «видео» – текстовый файл исполняемый браузером и весящий меньше 9 килобайт! И это не опечатка – видео измеряется в килобайтах.

Вы можете скачать этот файл и показывать на своём компьютере, а можете вставить на свою страницу!

Отдельное спасибо Михаилу Панову, который умеет проникнуть в суть любого алгоритма с чёткими правилами – будь то TeX, MetaPost или, как сегодня, SVG-анимация. Это умение, помноженное на великолепное знание геометрии и удивительное усердие писать ручками код, приводит к действительно чудесам!

Обратим внимание, что на новом сайте заработала пользующаяся неизменной популярностью интерактивная головоломка по теореме Пифагора.

Наслаждайтесь сами и показывайте другим:
красивое доказательство теоремы Пифагора https://etudes.ru/etudes/pythagorean-theorem-windmill-proof/ ,
интерактивная головоломка https://etudes.ru/etudes/pythagorean-theorem/ .

​​#реклама

Начало года — подходящее время для поиска первой работы или стажировки. На канале Стажировки от hh.ru каждый день появляются свежие предложения стажировок. Подписывайтесь, чтобы не упустить вакансию мечты.

https://t.me/hh_internships?utm_source=yandex&utm_medium=cpc&utm_campaign=geometrykanal

Материалы семинара «Теоремы Чевы и Менелая»
Алексей Сгибнев разобрал очередную тему курса геометрии 9 класса. Также была представлена интерактивная модель для понимания теоремы Менелая.

Видеозапись и другие материалы: https://vertical.sch-int.ru/seminar-2021-3-all/

Сапог Шварца. Пример многогранника, который вписан в цилиндр, но площадь его поверхности с ростом количества слоев не стремится к площади поверхности цилиндра, а стремится к бесконечности.

Можно также увеличивать количество вершин в одном слое. Если оно растет достаточно медленно, по сравнению с ростом количества слоев, то площадь каждого треугольника будет стремиться к нулю, но площадь поверхности по-прежнему будет стремиться к бесконечности.

Попробуйте такой сложить сами: http://mech.math.msu.su/~vvb/SchwartzLantern/SchwartzLantern.pdf

​​Научите ребенка превращать фантазии в концепции и проекты!

#реклама

На новом курсе для детей от GeekBrains он освоит практики креативного мышления, которые пригодятся в учёбе, творчестве и будущей профессии.

Смотрите подробности и оставляйте заявку на сайте.
Для детей от 6 до 11 лет.

Правильные многогранники обладают большим количеством симметрий и интересным образом могут быть вписаны друг в друга. На эту тему у нас уже есть фильмы:
Гармония правильных многогранников https://etudes.ru/etudes/platonic-solids-harmony/;
Тени https://etudes.ru/etudes/shadows/.

Но то – фильмы. А когда видишь «вживую» насколько большой тетраэдр можно после нескольких попыток поместить в куб, то это удивляет. Об этом сегодняшняя модель «Вместительный кубик» https://etudes.ru/models/cube-capacity/.

А сколько детей может поместиться в кубический метр? Если провести эксперимент, сделав безопасный куб с ребром в метр и без верхней грани, дети получат удовольствие, а вы — снова удивитесь результату!

Вот что получается

Оказалось, что в файле реализована не совсем конструкция сапога Шварца.

У сапога Шварца в каждом перпендикулярном сечении, проходящем через вершины, расположен правильный n-угольник. Два соседних n-угольника повернуты так, что вершины одного расположены над серединами сторон другого.

При проекции сапога на основание цилиндра получится правильный 2n-угольник.
Конструкция, файл которой дан выше, дает 7-угольник. То есть вершины расположены не в плоскостях, параллельных основаниям, а на винтовой линии, идущей по поверхности цилиндра.

Но вау-эффект от собраной модели не меньше.

#задача

Если строить сапог Шварца, вписывая в основание правильный n-угольник, какой угол при вершине будет у треугольных граней сапога?

Добавим сюда малярный парадокс из «Кванта»: «с одной стороны необходимо бесконечное количество краски, а с другой стороны ее потребуется лишь 2•pi см³» http://kvant.mccme.ru/1986/08/malyarnyj_paradoks.htm

И о том же в брошюре «Что не так? Математические парадоксы и софизмы» С.М.Львовского. Ее можно купить в издательстве: https://biblio.mccme.ru/node/11775/shop

Вот какой сапог у меня получился из правильного треугольника.

В пространстве расположены два тетраэдра. Для любой плоскости, проекции тетраэдров на неё либо обе являются треугольниками, либо обе являются четырехугольниками. Докажите, что тетраэдры подобны.

— вот такая, например, забавная задача с идущей сейчас Летней конференции Турнира городов

#задача

Задача, вернувшаяся с того света: Нарисовали треугольник ABC,  отметили точки М1 — середину стороны ВС, L1 — основание биссектрисы из вершины А и ортоцентр Н. Потом всё, кроме этих трёх точек стёрли. Как восстановить треугольник по этим трём точкам?

Почему эта задача была похоронена, а потом возвращена к жизни (а заодно её решение) вы узнаете на семинаре учителей математики в среду в 19:00 по Москве.
https://mccme.ru/nir/seminar/

Вчерашняя тема оказалась не исчерпана. Уже после того, как опубликовал объявление о семинаре, написал следующий текст. Любите геометрию. is.gd/JKDj28