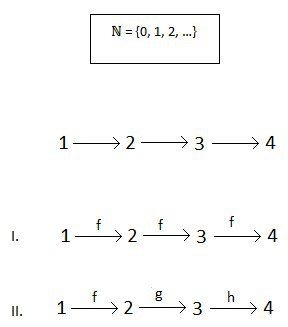
Всем привет. Чёрт, я тут опять пытался понять теорию категорий...) сорян, за мои тупые вопросы, ну,
Вот например, у меня было совершенно обычное множество, множество натуральных чисел, и я захотел, чтобы каждый элемент этого множества был объектом некой категории. (так вообще можно? И как это называеться вообще? "доведение множества до категории"?)
И мол, если попробовать это зарисовать в диаграмме и проименовать морфизмы, то какой вариант правильный, 1ый или 2ой?
(Вообще такая запись валидная как в 1ом? Например если я нарисую
A -(f)-> B -(f)-> C
, то это будет валидная запись что A,B и C одно и тоже, или недопустимо так зарисовывать, потому что разными буквами я указываю что это разные объекты?)
И если не 1-ый, то почему?
Ведь морфизм f можно интерпретировать как функцию (+1), а (+1)1 это 2, и (+1)2 это 3... надеюсь мысль понятна...
