Oℕ
1 -(f)-> 2 -(f)-> 3, где f = (<=) и тогда опять получается что 1=2=3,как и в диалоге выше я уточнял. Или между 1 и 2, и 2 и 3 это разные (<=) ?Size: a a a
Oℕ
1 -(f)-> 2 -(f)-> 3, где f = (<=) и тогда опять получается что 1=2=3,как и в диалоге выше я уточнял. Или между 1 и 2, и 2 и 3 это разные (<=) ?L🇷
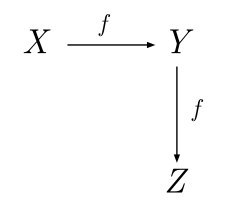
Oℕ
L🇷
f : A->B , а потом я ещё скажу что f: B->C, то разьве это не значит что A==B и B==C а потом и A==C ? Мол что это одни и теже объекты в категории?Oℕ
f : A->B , а потом я ещё скажу что f: B->C, то разьве это не значит что A==B и B==C а потом и A==C ? Мол что это одни и теже объекты в категории?Oℕ
ЗП
f : A->B , а потом я ещё скажу что f: B->C, то разьве это не значит что A==B и B==C а потом и A==C ? Мол что это одни и теже объекты в категории?Oℕ
L🇷
L🇷
L🇷
L🇷
Oℕ
L🇷
Oℕ
L🇷
Oℕ
L🇷
Oℕ
Oℕ