CH
Size: a a a
2020 February 24
Огромное спасибо!
CH
Ктстати, может кто видел (стыкующийся с программой Вербицкого) "манифест" http://lj.rossia.org/~dmitri_pavlov/9543.html?nc=198
Довольно старенький, но, по-моему, в наших реалиях такие подходы к ряду областей представляют крайний интерес
Может кто знает, где найти литературу? Особенно интересно про бескоординатную линейную алгебру
Довольно старенький, но, по-моему, в наших реалиях такие подходы к ряду областей представляют крайний интерес
Может кто знает, где найти литературу? Особенно интересно про бескоординатную линейную алгебру
AG
про бескоординатную линейку у акслера есть учебник
2020 February 25
NI
Вечная тема ;-)
Bicategories of spans as generic bicategories
Charles Walker
https://arxiv.org/abs/2002.10334
In a bicategory of spans (an example of a 'generic bicategory') the factorization of a span (s,t) as the span (s,1) followed by (1,t) satisfies a simple universal property with respect to all factorizations in terms of the generic bicategory structure.
Here we show that this universal property can in fact be used to characterize bicategories of spans.
This characterization of spans is very different from the others in that it does not mention any adjointness conditions within the bicategory.
#paper
Bicategories of spans as generic bicategories
Charles Walker
https://arxiv.org/abs/2002.10334
In a bicategory of spans (an example of a 'generic bicategory') the factorization of a span (s,t) as the span (s,1) followed by (1,t) satisfies a simple universal property with respect to all factorizations in terms of the generic bicategory structure.
Here we show that this universal property can in fact be used to characterize bicategories of spans.
This characterization of spans is very different from the others in that it does not mention any adjointness conditions within the bicategory.
#paper
L🇷
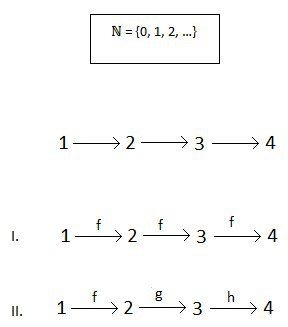
Всем привет. Чёрт, я тут опять пытался понять теорию категорий...) сорян, за мои тупые вопросы, ну,
Вот например, у меня было совершенно обычное множество, множество натуральных чисел, и я захотел, чтобы каждый элемент этого множества был объектом некой категории. (так вообще можно? И как это называеться вообще? "доведение множества до категории"?)
И мол, если попробовать это зарисовать в диаграмме и проименовать морфизмы, то какой вариант правильный, 1ый или 2ой?
(Вообще такая запись валидная как в 1ом? Например если я нарисую
, то это будет валидная запись что A,B и C одно и тоже, или недопустимо так зарисовывать, потому что разными буквами я указываю что это разные объекты?)
И если не 1-ый, то почему?
Ведь морфизм f можно интерпретировать как функцию (+1), а (+1)1 это 2, и (+1)2 это 3... надеюсь мысль понятна...
Вот например, у меня было совершенно обычное множество, множество натуральных чисел, и я захотел, чтобы каждый элемент этого множества был объектом некой категории. (так вообще можно? И как это называеться вообще? "доведение множества до категории"?)
И мол, если попробовать это зарисовать в диаграмме и проименовать морфизмы, то какой вариант правильный, 1ый или 2ой?
(Вообще такая запись валидная как в 1ом? Например если я нарисую
A -(f)-> B -(f)-> C
, то это будет валидная запись что A,B и C одно и тоже, или недопустимо так зарисовывать, потому что разными буквами я указываю что это разные объекты?)
И если не 1-ый, то почему?
Ведь морфизм f можно интерпретировать как функцию (+1), а (+1)1 это 2, и (+1)2 это 3... надеюсь мысль понятна...
A
> И если не 1-ый, то почему?
Потому что объект по отношению к морфизму — это "область определения" или "область значений" функции, а не конкретное значение аргумента.
Потому что объект по отношению к морфизму — это "область определения" или "область значений" функции, а не конкретное значение аргумента.
H
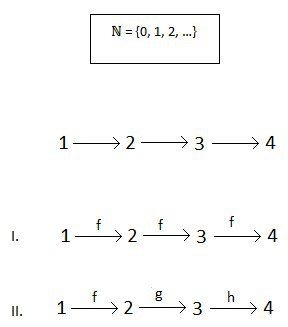
Всем привет. Чёрт, я тут опять пытался понять теорию категорий...) сорян, за мои тупые вопросы, ну,
Вот например, у меня было совершенно обычное множество, множество натуральных чисел, и я захотел, чтобы каждый элемент этого множества был объектом некой категории. (так вообще можно? И как это называеться вообще? "доведение множества до категории"?)
И мол, если попробовать это зарисовать в диаграмме и проименовать морфизмы, то какой вариант правильный, 1ый или 2ой?
(Вообще такая запись валидная как в 1ом? Например если я нарисую
, то это будет валидная запись что A,B и C одно и тоже, или недопустимо так зарисовывать, потому что разными буквами я указываю что это разные объекты?)
И если не 1-ый, то почему?
Ведь морфизм f можно интерпретировать как функцию (+1), а (+1)1 это 2, и (+1)2 это 3... надеюсь мысль понятна...
Вот например, у меня было совершенно обычное множество, множество натуральных чисел, и я захотел, чтобы каждый элемент этого множества был объектом некой категории. (так вообще можно? И как это называеться вообще? "доведение множества до категории"?)
И мол, если попробовать это зарисовать в диаграмме и проименовать морфизмы, то какой вариант правильный, 1ый или 2ой?
(Вообще такая запись валидная как в 1ом? Например если я нарисую
A -(f)-> B -(f)-> C
, то это будет валидная запись что A,B и C одно и тоже, или недопустимо так зарисовывать, потому что разными буквами я указываю что это разные объекты?)
И если не 1-ый, то почему?
Ведь морфизм f можно интерпретировать как функцию (+1), а (+1)1 это 2, и (+1)2 это 3... надеюсь мысль понятна...
Множество натуральных чисел является объектом ( смотри выше ). Возьмем его как А, то тогда у тебя морфизм идет из А в А. Ты же взял объекты как область значений, что не является верным.
> И как это называеться вообще? "доведение множества до категории"?)
Свободная категория порожденная ( здесь название структуры которую ты довел до категории ).
P.S. сам начинающий, так что могу ошибаться.
> И как это называеться вообще? "доведение множества до категории"?)
Свободная категория порожденная ( здесь название структуры которую ты довел до категории ).
P.S. сам начинающий, так что могу ошибаться.
A
Hmm
Множество натуральных чисел является объектом ( смотри выше ). Возьмем его как А, то тогда у тебя морфизм идет из А в А. Ты же взял объекты как область значений, что не является верным.
> И как это называеться вообще? "доведение множества до категории"?)
Свободная категория порожденная ( здесь название структуры которую ты довел до категории ).
P.S. сам начинающий, так что могу ошибаться.
> И как это называеться вообще? "доведение множества до категории"?)
Свободная категория порожденная ( здесь название структуры которую ты довел до категории ).
P.S. сам начинающий, так что могу ошибаться.
Можно объектами и каждое натуральное число по отдельности сделать
A
Hmm
Множество натуральных чисел является объектом ( смотри выше ). Возьмем его как А, то тогда у тебя морфизм идет из А в А. Ты же взял объекты как область значений, что не является верным.
> И как это называеться вообще? "доведение множества до категории"?)
Свободная категория порожденная ( здесь название структуры которую ты довел до категории ).
P.S. сам начинающий, так что могу ошибаться.
> И как это называеться вообще? "доведение множества до категории"?)
Свободная категория порожденная ( здесь название структуры которую ты довел до категории ).
P.S. сам начинающий, так что могу ошибаться.
Свободная категория по графу порождается. По множеству это никак не называется, посольку не имеет смысла — кроме объектов нужно задавать морфизмы (и они как раз главную роль в категории играют). Разве что есть понятие "дискретной категории", когда никаких морфизмов, кроме id, нет.
H
Можно объектами и каждое натуральное число по отдельности сделать
не знал, что с множеством значений это тоже работает, спасибо
A
Hmm
не знал, что с множеством значений это тоже работает, спасибо
Объекты могут чем угодно являться
H
Еще раз спасибо :)
L🇷
Свободная категория по графу порождается. По множеству это никак не называется, посольку не имеет смысла — кроме объектов нужно задавать морфизмы (и они как раз главную роль в категории играют). Разве что есть понятие "дискретной категории", когда никаких морфизмов, кроме id, нет.
Просто, я как бы хотел "раскрыть" объект категории, на примере категории множества, где объекты это множества
L🇷
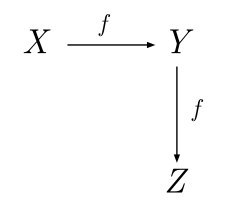
в общем, ладно, но у меня всё равно вопрос, я могу записать так, имея ввиду что X Y и Z это одно и тоже?
KV
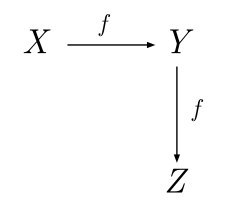
в общем, ладно, но у меня всё равно вопрос, я могу записать так, имея ввиду что X Y и Z это одно и тоже?
Да, но кого Вы пытаетесь этим запутать?
L🇷
Да, но кого Вы пытаетесь этим запутать?
да никого) просто вот я задался вопросом выше, а там очень специфичная запись у меня) И я подумал мол " 1-ый вариант вообще валдиный? тогда все объекты это одно и тоже..."
A
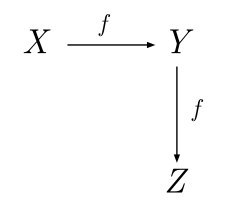
в общем, ладно, но у меня всё равно вопрос, я могу записать так, имея ввиду что X Y и Z это одно и тоже?
такое f называется эндоморфизмом btw
L🇷
такое f называется эндоморфизмом btw
да, но мне в данном примере важно было значение букв, мол в такой нотации каждая буква это прям что-то уникальное, или они могут быть чем-то одним и темже




