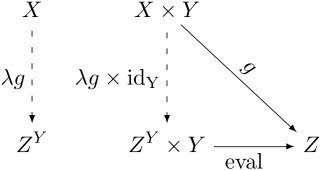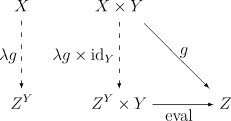МБ
Size: a a a
2019 October 30
и как она определена?
Ну, в Hask, видимо, она определена, как каррирование. А КАМ она определена, как защита куска кода от исполнения. Но вот в этом месте я не понимаю, что такое сам морфизм.
YS
а что здесь X и Z^Y? одно из них функции, а другое — коды функций? что из них что?
извините, я, наверно, совсем не разбираюсь в ТК и задаю глупые вопросы, но издалека λg выглядит как что-то вроде соответствия между кодом функции и семантикой.
и каррирования здесь я не вижу совсем
извините, я, наверно, совсем не разбираюсь в ТК и задаю глупые вопросы, но издалека λg выглядит как что-то вроде соответствия между кодом функции и семантикой.
и каррирования здесь я не вижу совсем
NI
Не подскажете ли, где можно почитать философские (ну, качественные) объяснения того, что такое экспоненциал? Я вот чего не понимаю.
Возьмём категорию Hask. Объекты — это типы, типизированные термы - это морфизмы. Но что тогда такое
Что бы такое почитать, чтобы прояснить все детали? С абстрактной точки зрения, конечно, определение очевидно. Но вот концептуально я плыву.
Возьмём категорию Hask. Объекты — это типы, типизированные термы - это морфизмы. Но что тогда такое
lambda? Отображение, переводящее терм в форме lambda (x, y) ... в терм в форме lambda x. lambda y ... и "сохранение" его во множестве a -> b -> c? То есть, чисто текстовое такое преобразование? Но это как-то расходится с тем, что про lambda пишут в большинстве других случаев, где lambda — это нечто вроде конструктора кода вычисления.Что бы такое почитать, чтобы прояснить все детали? С абстрактной точки зрения, конечно, определение очевидно. Но вот концептуально я плыву.
Это множество стрелок a→b с операцией
eval : (a→b)×a → b
eval : (a→b)×a → b
YS
да, судя по https://ru.wikipedia.org/wiki/%D0%AD%D0%BA%D1%81%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB, λ здесь обозначено каррирование
YS
а что здесь X и Z^Y? одно из них функции, а другое — коды функций? что из них что?
извините, я, наверно, совсем не разбираюсь в ТК и задаю глупые вопросы, но издалека λg выглядит как что-то вроде соответствия между кодом функции и семантикой.
и каррирования здесь я не вижу совсем
извините, я, наверно, совсем не разбираюсь в ТК и задаю глупые вопросы, но издалека λg выглядит как что-то вроде соответствия между кодом функции и семантикой.
и каррирования здесь я не вижу совсем
короче, всё наоборот. нет здесь никакой семантики и кода. только каррирование
YS
в Хаске экспоненциал — это (->), eval = flip id
NI
в Хаске экспоненциал — это (->), eval = flip id
Ну да. Чуть перефразирую подлиньше то "философское" объяснение, что написал выше.
Экспоненциал, это множество всех стрелок между a и b, обозначается через bª.
К нему есть приспособа eval, которая берёт элемент этого множества bª (который является стрелкой из a в b), элемент из a и применяет эту стрелку к этому элементу.
То есть, имеет тип eval : bª × a → b
Объект вместе с eval'ом должны быть универсальными среди всех стрелок такого типа.
Т.е., в некотором смысле, bª должно быть"наибольшим" множеством, множеством всех-всех таких стрелок.
Экспоненциал, это множество всех стрелок между a и b, обозначается через bª.
К нему есть приспособа eval, которая берёт элемент этого множества bª (который является стрелкой из a в b), элемент из a и применяет эту стрелку к этому элементу.
То есть, имеет тип eval : bª × a → b
Объект вместе с eval'ом должны быть универсальными среди всех стрелок такого типа.
Т.е., в некотором смысле, bª должно быть"наибольшим" множеством, множеством всех-всех таких стрелок.
NI
В хаскеле, это сопряжение соответствует каррированию-декаррированию.
YS
В хаскеле, это сопряжение соответствует каррированию-декаррированию.
какое сопряжение?
МБ
какое сопряжение?
Экспоненциала и произведения
NI
какое сопряжение?
Тут написано —
https://ru.wikipedia.org/wiki/Экспоненциал
Если экспоненциал zʸ существует для всех z в C, то функтор, отправляющий z в zʸ является правым сопряжённым к [_] × y.
https://ru.wikipedia.org/wiki/Экспоненциал
Если экспоненциал zʸ существует для всех z в C, то функтор, отправляющий z в zʸ является правым сопряжённым к [_] × y.
МБ
В хаскеле, это сопряжение соответствует каррированию-декаррированию.
Ну, то есть, в Hask, стрелками являются термы. Равенство между стрелками -- это равенство нормальных форм, а
lambda - каррирование?МБ
Каррирование, как перевод терма
lambda (x, y) ... в терм lambda x. lambda y ...?NI
Каррирование, как перевод терма
lambda (x, y) ... в терм lambda x. lambda y ...?Да.
NI
Равенство можно по-разному определять ;-)
Но наверное, равенство нормальных форм сойдёт, хоть его и не всегда можно вычислить.
Но наверное, равенство нормальных форм сойдёт, хоть его и не всегда можно вычислить.
NI
Каррирование, как перевод терма
lambda (x, y) ... в терм lambda x. lambda y ...?Было бы проще про хаскель хаскелевским синтаксисом, он не очень громоздкий ;-)
МБ
Ускользает от меня тут то, что многие авторы называют "computation".
МБ
Было бы проще про хаскель хаскелевским синтаксисом, он не очень громоздкий ;-)
Я специально для себя, чтобы не зажигать лишние ассоциации :)
NI
Каррированная форма функции от двух преременных, это x→zʸ.
Или в хаскелевском синтаксисе, x→(y→z), ну а учитывая ассоциативность, можно и без скобок x→y→z.
Декаррированная форма этой функции, это x×y→z
Просто уточнил.
Или в хаскелевском синтаксисе, x→(y→z), ну а учитывая ассоциативность, можно и без скобок x→y→z.
Декаррированная форма этой функции, это x×y→z
Просто уточнил.
МБ
Равенство можно по-разному определять ;-)
Но наверное, равенство нормальных форм сойдёт, хоть его и не всегда можно вычислить.
Но наверное, равенство нормальных форм сойдёт, хоть его и не всегда можно вычислить.
Ну, обычно же, это равенство устанавливается через сведение термов к чему-то одинаковому по правилам редукции. Ну, эти знаменитые equational reasoning. Ну, да. Хорошо. Наверное, равенство надо устанавливать так: термы сводятся к чему-то одному, тогда стрелки равны.