D
Size: a a a
2021 June 19
Ошибка максимальная какая?
А
Кстати я вот немного сейчас помедитировал с калькулятором над формулами синуса, и получился довольно неплохой вариант:
Угол из промежутка [-pi/2, pi/2] делите на 5,
Раскладываем синус в ряд (нужно всего 3 слагаемых)
sin(x) = x - x³/6 + x⁵/120
А потом результат подставляем в формулу пятерного угла
sin(5a) = 5 sin(a) - 20 sin³(a) + 16 sin⁵(a)
Для значения 1.58 результат совпадает до 8 значащих цифр. Для меньших углов погрешность судя по всему будет еще меньше, ибо фоомула пятерного угла работает всегда, а точность приближения рядом увеличивается. Если вам до 7 знака - вот вам отличный вариант, даже 1 "про запас"
Угол из промежутка [-pi/2, pi/2] делите на 5,
Раскладываем синус в ряд (нужно всего 3 слагаемых)
sin(x) = x - x³/6 + x⁵/120
А потом результат подставляем в формулу пятерного угла
sin(5a) = 5 sin(a) - 20 sin³(a) + 16 sin⁵(a)
Для значения 1.58 результат совпадает до 8 значащих цифр. Для меньших углов погрешность судя по всему будет еще меньше, ибо фоомула пятерного угла работает всегда, а точность приближения рядом увеличивается. Если вам до 7 знака - вот вам отличный вариант, даже 1 "про запас"
A
смортя где. чем ближе к нулю, тем меньше.
D
Понял
D
Ну у нуля как раз можно считать, а дальше куски размножить
D
И норм
A
там можно степени числителя и знаменателя менять, смотреть, что получится.
A
а забавный вариант!
D
А коэффициенты? Тоже наверное
D
Жесть
АА
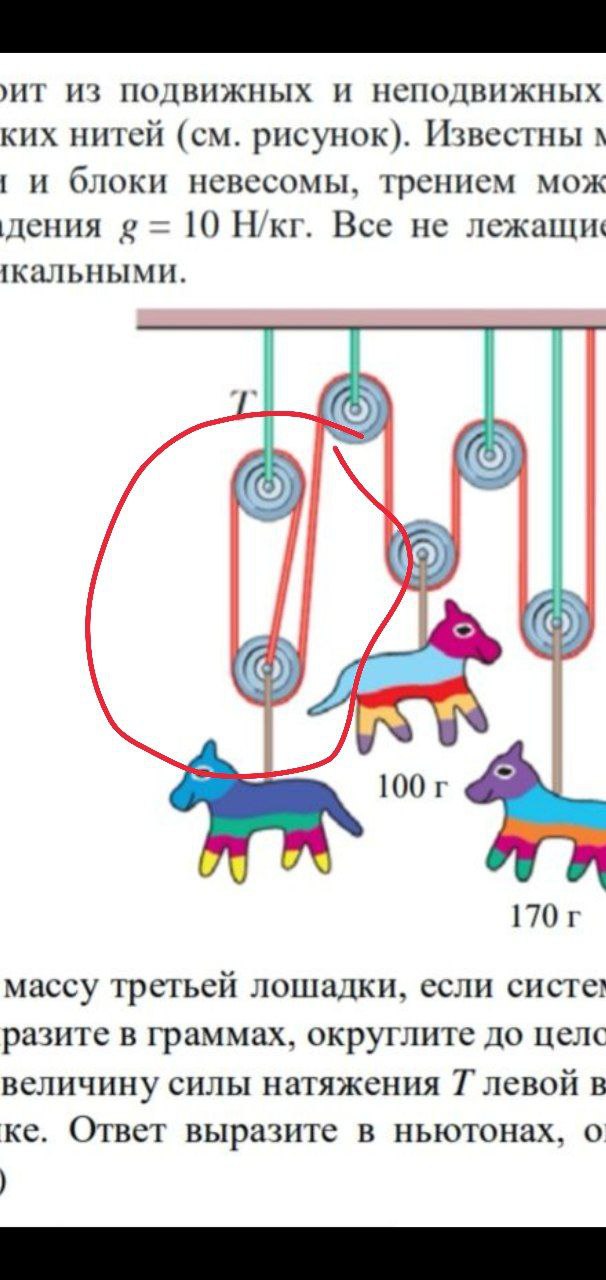
Всем привет, я не прошу решения. Лишь хочу узнать, что это значит. Я имею ввиду нить, которая проходит через блок. Заранее спасибо.
A
так коэффициенты она подберёт, в зависимости от этих степеней.
D
Понял
TL
Она не проходит через блок, она прикреплена к центру блока
A
видимо, там есть такое ушко, в которое продели.
TL
Вроде того
A
вопрос в том, как прикреплена. на неё там действует только горизонтальная сила?
АА
конструкция в равновесии