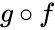VP
Size: a a a
2021 March 29
Вообще интересно осознавать, что умножение и сложение скорей разные,чем похожи
VP
Нас учили его через сложение выражать
VP
А тут Добрый вечер, умножьте на 1.5
O
Вот меня иной раз ночью мучает вопрос:
Можно ли придумать операцию, сходную по всем свойствам с + и * , но чтобы для неё нулем было число 2.
Можно ли придумать операцию, сходную по всем свойствам с + и * , но чтобы для неё нулем было число 2.
т.е. чтобы 2 было нейтральным элементом для + и поглощающим для *?
O
на каком множестве?
DF
Дядя, я вообще-то не настоящий теоретик категорий. Я просто головоломку на стройке нашёл...
Попробую переформулировать:
Есть две общеизвестные операции + и *. Да, в чем-то они похожи, в чем-то разные. Эта «парочка» являет себя в разных алгебрах: объединение/пересечение множеств, OR/AND и т.п. В разных алгебрах они могут иметь или не иметь кое-какие свойства (произведение матриц не коммутативно). Кроме этого можно взять во внимание то, что:
а) Вторая выражается через первую.
б) нейтральный элемент для одной - 0, а для другой - 1.
То хочется, чтобы была некая закономерность, согласно которой можно получить третью операцию (вернее пару: операция ?, нейтральный элемент X).
При этом желательно, чтобы
- операция ? выражалась бы через * также просто и изящно как * выражается через +.
- аналогично: X находится в таком же (неизвестно в каком именно, но желательно в каком-то простом и изящном) отношении с числом 1, как число 1 соотносится с числом 0.
Есть понятие гипероперации, но это не то. Так * является гипероперацией над +, но если взять гипероперацию над * - то самое «возведение в степень» (которая, кстати, в алгебре матриц определена только для квадратных матриц), то нейтральным элементом для возведения в степень является ровно то же число 1, что и для самой операции *, а это не то, чего нам хотелось бы. Напомню: хочется, чтобы нейтр. элемент третьей операции был в том же отношении с нейтр. элементом второй операции, в каком нейтр. элемент второй операции соотносится с нейтр. элементом первой операции.
Эк меня понесло...
Попробую переформулировать:
Есть две общеизвестные операции + и *. Да, в чем-то они похожи, в чем-то разные. Эта «парочка» являет себя в разных алгебрах: объединение/пересечение множеств, OR/AND и т.п. В разных алгебрах они могут иметь или не иметь кое-какие свойства (произведение матриц не коммутативно). Кроме этого можно взять во внимание то, что:
а) Вторая выражается через первую.
б) нейтральный элемент для одной - 0, а для другой - 1.
То хочется, чтобы была некая закономерность, согласно которой можно получить третью операцию (вернее пару: операция ?, нейтральный элемент X).
При этом желательно, чтобы
- операция ? выражалась бы через * также просто и изящно как * выражается через +.
- аналогично: X находится в таком же (неизвестно в каком именно, но желательно в каком-то простом и изящном) отношении с числом 1, как число 1 соотносится с числом 0.
Есть понятие гипероперации, но это не то. Так * является гипероперацией над +, но если взять гипероперацию над * - то самое «возведение в степень» (которая, кстати, в алгебре матриц определена только для квадратных матриц), то нейтральным элементом для возведения в степень является ровно то же число 1, что и для самой операции *, а это не то, чего нам хотелось бы. Напомню: хочется, чтобы нейтр. элемент третьей операции был в том же отношении с нейтр. элементом второй операции, в каком нейтр. элемент второй операции соотносится с нейтр. элементом первой операции.
Эк меня понесло...
DF
Можно очень коротко сформулировать в стиле Стивена Хокинга: Почему их всего две?
a
Дядя, я вообще-то не настоящий теоретик категорий. Я просто головоломку на стройке нашёл...
Попробую переформулировать:
Есть две общеизвестные операции + и *. Да, в чем-то они похожи, в чем-то разные. Эта «парочка» являет себя в разных алгебрах: объединение/пересечение множеств, OR/AND и т.п. В разных алгебрах они могут иметь или не иметь кое-какие свойства (произведение матриц не коммутативно). Кроме этого можно взять во внимание то, что:
а) Вторая выражается через первую.
б) нейтральный элемент для одной - 0, а для другой - 1.
То хочется, чтобы была некая закономерность, согласно которой можно получить третью операцию (вернее пару: операция ?, нейтральный элемент X).
При этом желательно, чтобы
- операция ? выражалась бы через * также просто и изящно как * выражается через +.
- аналогично: X находится в таком же (неизвестно в каком именно, но желательно в каком-то простом и изящном) отношении с числом 1, как число 1 соотносится с числом 0.
Есть понятие гипероперации, но это не то. Так * является гипероперацией над +, но если взять гипероперацию над * - то самое «возведение в степень» (которая, кстати, в алгебре матриц определена только для квадратных матриц), то нейтральным элементом для возведения в степень является ровно то же число 1, что и для самой операции *, а это не то, чего нам хотелось бы. Напомню: хочется, чтобы нейтр. элемент третьей операции был в том же отношении с нейтр. элементом второй операции, в каком нейтр. элемент второй операции соотносится с нейтр. элементом первой операции.
Эк меня понесло...
Попробую переформулировать:
Есть две общеизвестные операции + и *. Да, в чем-то они похожи, в чем-то разные. Эта «парочка» являет себя в разных алгебрах: объединение/пересечение множеств, OR/AND и т.п. В разных алгебрах они могут иметь или не иметь кое-какие свойства (произведение матриц не коммутативно). Кроме этого можно взять во внимание то, что:
а) Вторая выражается через первую.
б) нейтральный элемент для одной - 0, а для другой - 1.
То хочется, чтобы была некая закономерность, согласно которой можно получить третью операцию (вернее пару: операция ?, нейтральный элемент X).
При этом желательно, чтобы
- операция ? выражалась бы через * также просто и изящно как * выражается через +.
- аналогично: X находится в таком же (неизвестно в каком именно, но желательно в каком-то простом и изящном) отношении с числом 1, как число 1 соотносится с числом 0.
Есть понятие гипероперации, но это не то. Так * является гипероперацией над +, но если взять гипероперацию над * - то самое «возведение в степень» (которая, кстати, в алгебре матриц определена только для квадратных матриц), то нейтральным элементом для возведения в степень является ровно то же число 1, что и для самой операции *, а это не то, чего нам хотелось бы. Напомню: хочется, чтобы нейтр. элемент третьей операции был в том же отношении с нейтр. элементом второй операции, в каком нейтр. элемент второй операции соотносится с нейтр. элементом первой операции.
Эк меня понесло...
Возможность выразить × через + это не более чем совпадение, так что не стоит надеяться найти этому обобщение.
a
Можно очень коротко сформулировать в стиле Стивена Хокинга: Почему их всего две?
× это по сути произведение в категории множеств; + это по сути копроизведение в ней же. Их всего две потому что такова жызнь.
DF
Во. Интересно.
O
& и | можно друг через друга выразить, в отличие от + и *, так что да, скорее совпадение
DF
Копроизведение...
DF
А произведение матриц выражается через сумму матриц?
DF
& и | можно друг через друга выразить, в отличие от + и *, так что да, скорее совпадение
Только с привлечением NOT, не так ли?
DF
А произведение матриц выражается через сумму матриц?
Кажется выражается, но очень долго.
O
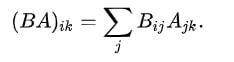
в каком-то роде да
DF
× это по сути произведение в категории множеств; + это по сути копроизведение в ней же. Их всего две потому что такова жызнь.
Да. Из Википедии:
Копроизведение объектов двойственно их произведению, то есть определение копроизведения можно получить из определения произведения обращением всех стрелок. Тем не менее, во многих категориях произведение и копроизведение объектов разительно отличаются.
И тут новая формулировка головоломки: почему лишь «двойственно»? Где третий?
Копроизведение объектов двойственно их произведению, то есть определение копроизведения можно получить из определения произведения обращением всех стрелок. Тем не менее, во многих категориях произведение и копроизведение объектов разительно отличаются.
И тут новая формулировка головоломки: почему лишь «двойственно»? Где третий?
O
как этот третий определить? у произведения есть две проекции, у суммы - две инъекции. что у третьего?
O
у стрелок есть два направления: туда и обратно. третьего направления нет