Телеграмм чат группы math

Пусть f: Rn→R, и все частные производные первого порядка функции f в каждой точке существуют и постоянны. Означает ли это, что функция f линейна?
Подскажите, пожалуйста, туда ли думаю: не означает, так как из существования всех частных производных не следует дифференцируемость, значит ф-ия может быть не непрерывной, значит, в силу непрерывность линейной ф-ии, f линейна только тогда, когда она непрерывна

источник

22:14пожаловаться #9

ИГ

Иоанн Гольден... in Physics.Math.Code

Как лучше всего представить список смежности в плюсах?
Сам не придумал пока ничего лучше чем словарь, где ключ - вершина, а значение - множество вершин

источник

22:25пожаловаться #10

Ivan Makovetskiy in Physics.Math.Code

Хэш-таблицей, например

источник

22:58пожаловаться #11

Ivan Makovetskiy in Physics.Math.Code

у кормена посмотрите, там на списках

источник

22:59пожаловаться #12

ИГ

Иоанн Гольден... in Physics.Math.Code

Хорошо, спасибо

источник

23:00пожаловаться #13

Carl Johnson in Physics.Math.Code

vector<vector<int>, n> G?

источник

23:13пожаловаться #14

Carl Johnson in Physics.Math.Code

или не катит

источник

23:13пожаловаться #15

ИГ

Иоанн Гольден... in Physics.Math.Code

Навигация будет сложнее
Пока так и не придумал ничего лучше, чем использовать в качестве ключа доступа - адрес вершины из которой исходят ребра
Для вложенного вектора получится сложнее навигация и редактирование.

источник

23:19пожаловаться #16

ИГ

Иоанн Гольден... in Physics.Math.Code

Потому что всем этим добром мне предстоит манипулировать в графическом окошке

источник

23:21пожаловаться #17

ИГ

Иоанн Гольден... in Physics.Math.Code

Стоп
Вы имели ввиду матрицу смежности?
Тоже можно, но не очень хочется
Потому что объекты хранятся в разных коллекциях
Я могу их закинуть все в один вектор, но у них у всех разные роли
Придется как-то выкручиваться с новой индексацией

источник

23:24пожаловаться #18

Denkova Veronika in Physics.Math.Code

cisco123

источник

23:28пожаловаться #19

Carl Johnson in Physics.Math.Code

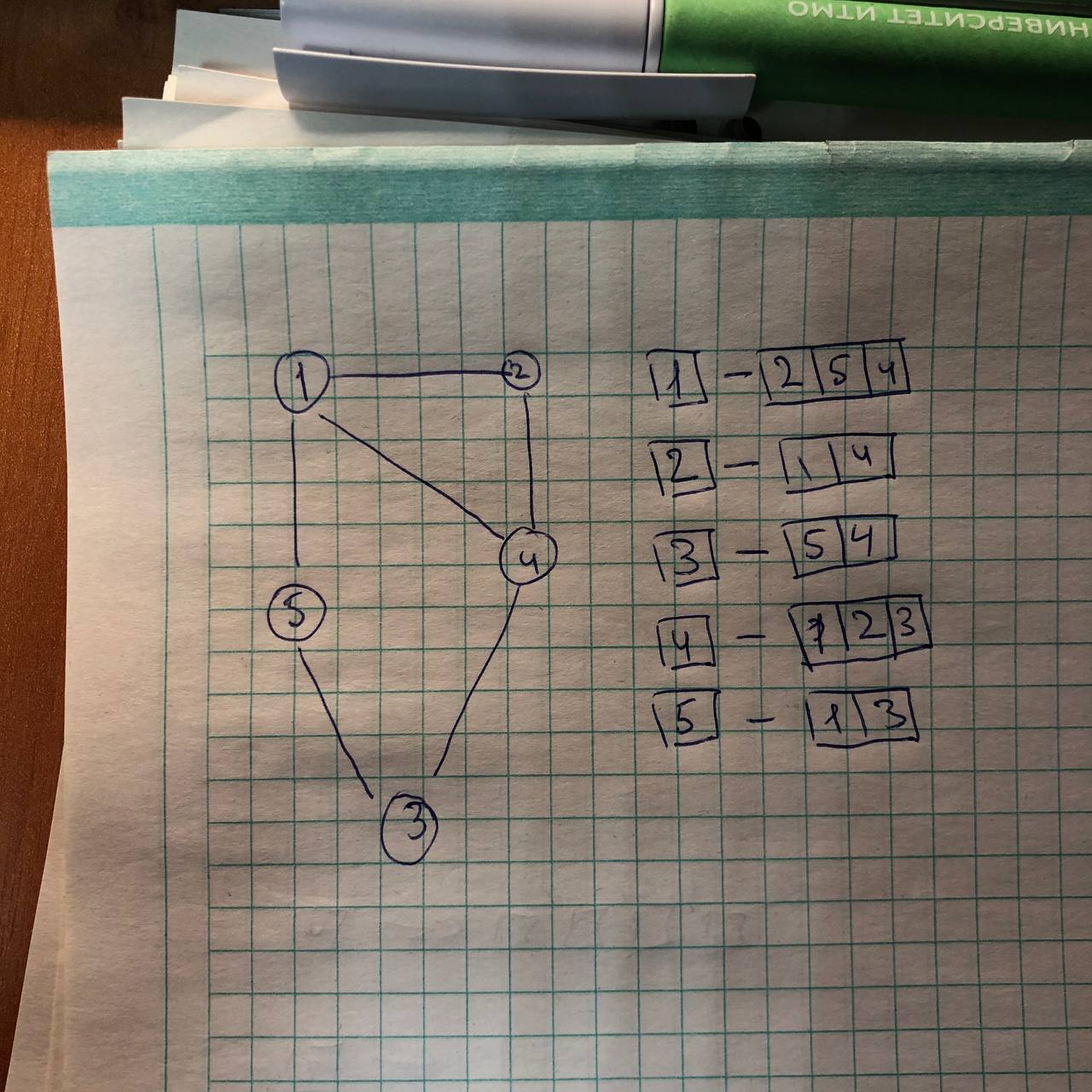
имел ввиду именно список смежности. структура будет выглядеть примерно так

источник

23:36пожаловаться #20