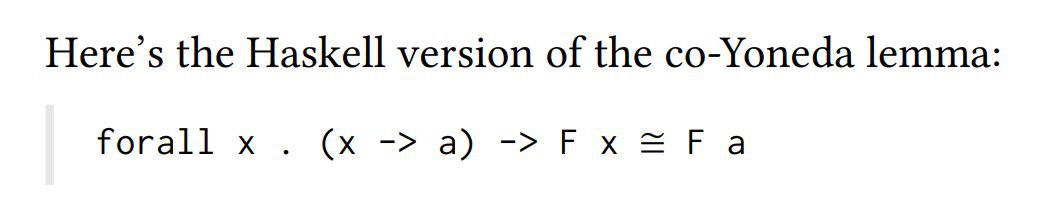IJ
Size: a a a
2019 December 22
неплохо бы наверное если бы был учебник, дающий теоркат как обобщение типов и линейки
chapter0 вроде близко
AZ
Это что, просто fmap?
МБ
неплохо бы наверное если бы был учебник, дающий теоркат как обобщение типов и линейки
В этой самой New Structures есть. При чём и алгебра, и логика. По тому и советую
YS
Это что, просто fmap?
не просто. это как бы универсальный fmap
AZ
так обычный фмап так же выглядит. Фиксируем F и для любой функци a -> b и F a даем F b
YS
обычный fmap зависит от x, а здесь штука, универсальная по x
AZ
не понимаю
AZ
fmap<A, B>(F<A>, A -> B): F<B>и A и B - любые типы
YS
так обычный фмап так же выглядит. Фиксируем F и для любой функци a -> b и F a даем F b
здесь требуется и обратное преобразование
AZ
хм, а можно пример когда обратного не будет?
AZ
а то я пытаюсь вспомнить типикал функторы типа мейби и так все это выполняется вроде
AG
В этой самой New Structures есть. При чём и алгебра, и логика. По тому и советую
а можно напомнить что за оно?
YS
fmap<A, B>(F<A>, A -> B): F<B>и A и B - любые типы
но здесь другой тип слева:
f<a>(template<x> (x -> a) -> F<x>) -> F<a>
f<a>(template<x> (x -> a) -> F<x>) -> F<a>
AZ
не вижу разницы
AZ
fmap в данном случае определяет семейство функций для любых A и B
МБ
а можно напомнить что за оно?
Линейщина, вычисления, типы, линейная алгебра
YS
а то я пытаюсь вспомнить типикал функторы типа мейби и так все это выполняется вроде
наверно, лемма правильная. напишите доказательство в общем виде. выразите
to :: (forall x . (x -> a) -> F x) -> F a
from :: F a -> (forall x . (x -> a) -> F x)
через fmapМБ
fmap в данном случае определяет семейство функций для любых A и B
fmap: (a -> b) -> (f a -> f b), а там: ((a -> b) -> f a) ~ f b
AZ
нет же. fmap == (a -> b) -> F a -> F b