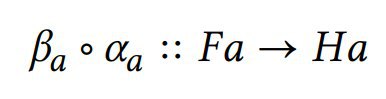ЕО
Size: a a a
2019 December 17
Воеводский брал тотальные языки, они скучнее
ЕО
Нормальная форма есть, можно на денотационную семантику вообще забить
МБ
Там, вроде, не особо важно. Ну, мы просто определяем понятие частично определённой функции через bottom, и всё.
YS
Надо определить "скучный". ТК, конечно, шире применяется.
даёт ли хаскельная монада полное понятие о категорной монаде?
ЕО
Там, вроде, не особо важно. Ну, мы просто определяем понятие частично определённой функции через bottom, и всё.
Ну нет, нельзя, порядок ещё нужен
ЕО
bottom меньше всех термов
ЕО
Нужно работать с (2,1)-категориями
ЕО
Задавать на стрелках топологии Скотта и т.д.
МБ
Я вот тут читаю Барендрегта, он пишет, что Скотт как раз и построил это самое с типами в категории решёток. Не знаю, правда, есть там type: type
МБ
даёт ли хаскельная монада полное понятие о категорной монаде?
Не знаю. Категорные монады, вроде как, возникают из алгебраических соображений о расширениях алгебраических структур (могу ошибаться, читал только у Ламбека в контексте категорной логики). Мне кажется, что списки или свободные монады это иллюстрируют.
ЕО
Я вот тут читаю Барендрегта, он пишет, что Скотт как раз и построил это самое с типами в категории решёток. Не знаю, правда, есть там type: type
Есть павердомен для этого. Просто домен это (0,1)-категория, а нам нужно всё-таки (2,1)-категория
МБ
Задавать на стрелках топологии Скотта и т.д.
Так топологии эти строятся, чтобы ограничить класс рассматриваемых функций. А потом разговор плавно переводится на язык этих функций. Не очень понятно, что может дать эта топология на homset-ах.
ЕО
Так топологии эти строятся, чтобы ограничить класс рассматриваемых функций. А потом разговор плавно переводится на язык этих функций. Не очень понятно, что может дать эта топология на homset-ах.
Ну, ограничение нам нужно, чтобы потом построить свободную структуру. Мы же хотим получить "максимальную" категорию, похожую на Hask
ЕО
@mbakhterev, вот, я придумал как перформулировать то, что я хочу сказать. Если мы будем смотреть на Hask не как на 1-категорию, а как на dcpo-enriched категорию, то эндофункторы над Hask будут вынуждены сохранять "вычислительную структуру" категории, а значит мы сможем любому эндофунктору сопоставить функтор-в-смысле-хаскеля
ЕО
И если в нашем Hask будет Type:Type, то мы сможем построить интернал-категорию internal Hask, рассмотреть на ней internal functors и показать, что они соответствуют обычным функторам нашего enriched Hask
МБ
Вопросы: Не идёт ли здесь речь о представимых функторах? Что подразумевается под "haskell-функтор"?
AZ
Всё-таки меня убивает, что рисуется b * a, а тип a -> b
CD
ох уж эти любители применения справа
МБ
Ну рисуйте
f;g -- f перед g.