Oℕ
Size: a a a
2018 February 22
какое видео?
тебе нельзя, там скала
DM
тебе нельзя, там скала
Рунар?
ЗП
Да какой тут нафиг Чёрч... Причём тут...
Построить категории Эйленберга-Мура и Клейсли для монады List и показать, где и как там возникают пары сопряжённых функторов, которые дают эту монаду.
Построить категории Эйленберга-Мура и Клейсли для монады List и показать, где и как там возникают пары сопряжённых функторов, которые дают эту монаду.
так! левое и правое сопряжение тут будет свободный и забывающий функторы переводящий из Set -> Mon и Mon -> Set?
Oℕ
вот и он как раз на сопряжения для лист монады подоспел
2018 February 23
к
я ведь правильно понимаю, что каждое естественное преобразование в пределах категории можно рассматривать как морфизм?
ЗП
я ведь правильно понимаю, что каждое естественное преобразование в пределах категории можно рассматривать как морфизм?
ну как бы да)
к
ну мне нужно было убедиться, а то я засомневался
ЗП
ну и еще натуральное преобразование может быть в точности до изоморфизма
к
я как-то раньше не акцентировал на этом внимание типа и так все понятно, а сейчас понял, что нет, не понятно
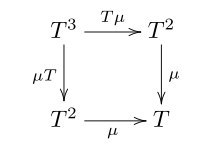
если верхний морфизм - T(mu), то что слева? Преобразование T^3 в T^4 и потом (T^2)^2->T^2?
если верхний морфизм - T(mu), то что слева? Преобразование T^3 в T^4 и потом (T^2)^2->T^2?
к
может тогда проще индексировать mu, типа mu_T, mu_(T^2)
ЗП
ну сверху это
T(T(T a)) -> fmap join -> T(T a)
T(T(T a)) -> fmap join -> T(T a)
ЗП
слева
T(T(T a)) -> join -> T(T a)
T(T(T a)) -> join -> T(T a)
AG
я ведь правильно понимаю, что каждое естественное преобразование в пределах категории можно рассматривать как морфизм?
как семейство морфизмов
к
ну конкретно mu_T - это один морфизм?
ЗП
ну конкретно mu_T - это один морфизм?
join походу
ЗП
а это один морфизм
к

я как-то раньше не акцентировал на этом внимание типа и так все понятно, а сейчас понял, что нет, не понятно
если верхний морфизм - T(mu), то что слева? Преобразование T^3 в T^4 и потом (T^2)^2->T^2?
если верхний морфизм - T(mu), то что слева? Преобразование T^3 в T^4 и потом (T^2)^2->T^2?
вот этот вопрос меня больше интересует
AG
слева
T(T( T(X) )) -> T( T(X) )AG
сверху T(
T(T( X )) ) -> T( T( X ))к
слева
T(T( T(X) )) -> T( T(X) )да-да, это я вижу по нодам, вопрос не в этом. Сверху мы применяем смапленый морфизм, то есть далем джоин внутри значения, там Tmu обозначает T(mu)
а что мы делаем слева? muT можно рассматривать как mu . T (Это же точно не mu_T или mu(T)), то есть сначала T^3 -> T^4, а потом (T^2)^2 -> T^2
а что мы делаем слева? muT можно рассматривать как mu . T (Это же точно не mu_T или mu(T)), то есть сначала T^3 -> T^4, а потом (T^2)^2 -> T^2



