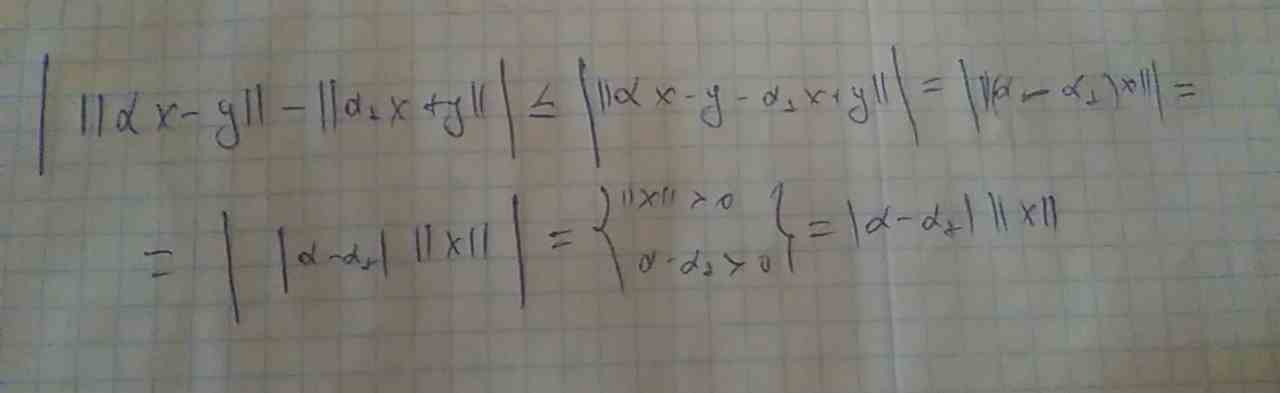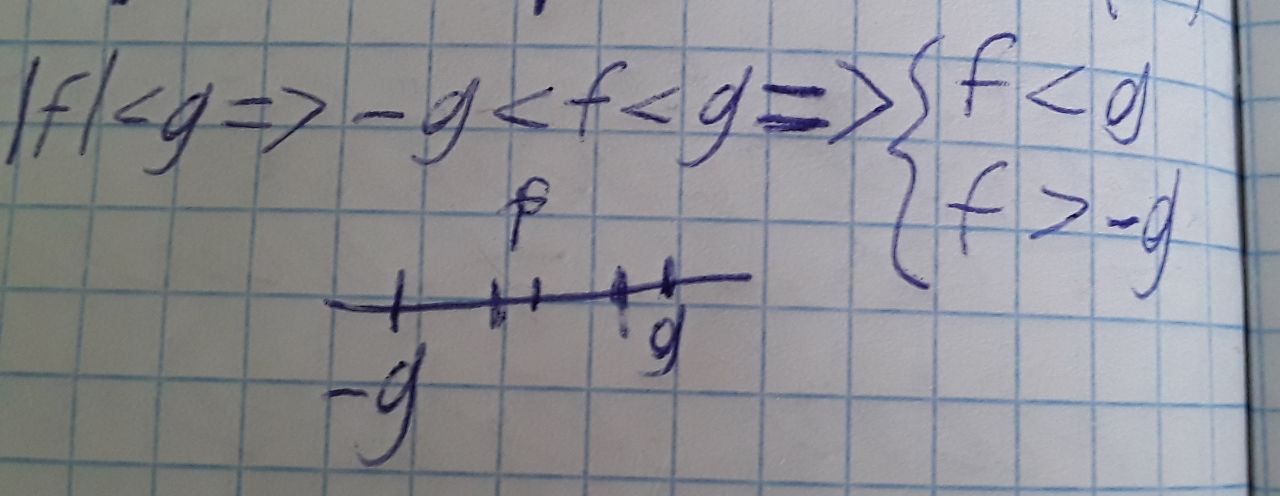DD
Size: a a a
2021 May 08
я понимаю. вы говорите о модуле в ПРАВОЙ части неравенства. Но у меня затык с модулем в ЛЕВОЙ части. Модуль в правой части на это не влияет
MA
Тогда так можно👇
MA
Левый модуль исчезают в последнем
PS
/gpt Список феменитивов для слова "математик":
1. Математикинея
2.
1. Математикинея
2.
M
Список феменитивов для слова "математик":
1. Математикинея
2. Амальгама диаматея Бёме или Гоголь с филуменом - таков набор образов, преподносимых нам различными культурами и течениями вплоть до сегодняшнего дня.
1. Математикинея
2. Амальгама диаматея Бёме или Гоголь с филуменом - таков набор образов, преподносимых нам различными культурами и течениями вплоть до сегодняшнего дня.
MA
А может математикелла
DD
модуль слева никуда не исчезает, т.к. он в следствии, которое надо доказать. Но то что на этой картинке это хорошее простое док-во))
PS
| ||x|| - ||y|| | <= ||x - y|| это следствие из неравенства треугольника
DD
да, но следствие тоже надо было доказать)
MA
Который?
MA
Этот?
DD
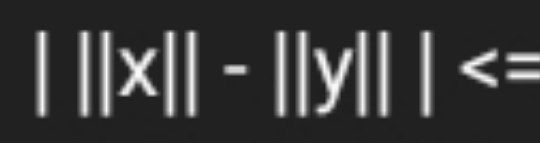
Я все вам пыталась донести про этот модуль в начале доказательства. Но на вашей последней картинке это соблюдено, так что все норм
DD
с ним и только с ним у меня возник затык изначально
MA
PS
Без ограничения общности ||x|| >= ||y||, и нужное неравенство получается из неравенства треугольника для y и x-y
DD
с чего это вдруг можно ||x|| >= ||y|| в общем случае?
PS
Ну, вернее так, если норма х не меньше нормы у, то неравенство треугольника для y и x-y, если меньше, то для x и y-x
PS
В первом случае получаете ||x-y|| >= ||x|| - ||y||
Во втором ||x-y|| >= ||y|| - ||x||, в итоге их можно объединить, навесив модуль
Во втором ||x-y|| >= ||y|| - ||x||, в итоге их можно объединить, навесив модуль
DD