Подскажите пожалуйста гармонические колебания это и есть свободные ,просто я запутался?

Нет. Свободные колебания характеризуются тем, что во время их совершения на них не действует вынуждающая сила. Как если бы вы один раз качелю толкнули и всё. При этом качеля когда-то остановится, а потому они не будут иметь вид гармонических - то есть, синусоиды, так как их амплитуда будет стремиться к нулю. Останавливаются качели потому, что на них действует сила трения, следовательно, если в системе вообще нет никаких сил сопротивления, колебания будут длиться бесконечно во времени, их ничего не будет тормозить, амплитуда не будет меняться, и получили бы снова гармонический вид. Но это гипотетическая ситуация, в реальности не осуществимая

А вот вынужденные колебания - это когда вы поддерживаете высоту, на которую поднимается качеля, постоянной, периодически толкая её - это и есть вынуждающая сила. Тогда колебания имеют форму синусоиды или косинусоиды во времени, и поэтому будут ещё и гармоническими

То есть, это разного рода понятия.
Гармонические/негармонические - форма, вынужденные/свободные - тип колебаний в зависимости от действия/недействия на них силы

А формулы у них же одинаковые?

Вот для свободных колебаний дифуравнение будет такое же как для гармонических.

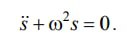
Она такая будет или нет?

Да, потому что единственное решение для дифуравнения без начальных/граничных условий достать невозможно

А в них и будет различие

Потому дифур один, а решений несколько, и они будут описывать разные колебания

Вы вот когда решаете дифуравнение, там же константы появляются. Так вот они же могут иметь совсем разный вид

Ну это на пальцах

А вообще... Вообще я не уверена, привыкла уже к уравнению волны в матфизике(

А это другое, сразу не заметила. Тут надо ещё подумать

Ну, производные здесь по времени?
Значит, начальные условия задавать будут

Так понимаю это

Если б были ещё производные по координате, то нужно было бы ещё краевые. Но это уже другая задача

Ну там не может быть одного решения, в любом случае. Из физического смысла

Где можно почитать, откуда взялись фундаментальные физические законы, например тот же второй закон Ньютона? В "Математических началах натуральной философии" в предисловии прямым текстом фраза "аксиомы Ньютона", но аксиомы должны быть интуитивно очевидны, иначе это теоремы. Только начал изучение физики, заучивать формулы нет никакого желания, хочется про каждую знать, откуда она берётся. Может, без знания математики на уровне диффуров это бесполезно или я не туда копаю?

А решение выходит не такое будет для свободных колебаний?

Нет, почему
Мы проходили на втором курсе классическую механику, и там каждая величина вводилась - можете познакомиться со вступлением. Вам пойдёт на украинском?

Если нет, лс, и я объясню в общих чертах, как я это понимаю, и как мне это донесли. Или здесь

.

Нет. Ну, как. Выходит, амплитуда А будет переменна. Тот самый случай с останавливающейся качелей.

Со временем она уменьшается по определённому закону. А в начальный момент времени пропорциональна величине силы ("толчка")

То есть, уравнение то же, но константа А - больше не константа, и её нужно найти

Пока бесполезно

уравнения Ньютона можно вывести из уравнений Лагранжа

или Гамильтона

или Шрёдингера