АД
Size: a a a
2021 June 11
Да, я подумал над этим. Выбирать стоит стандартный базис?
АГ
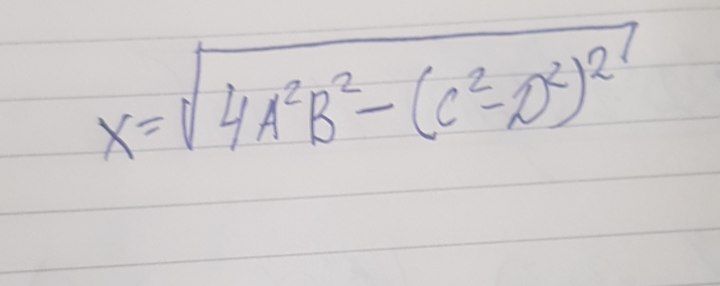
ребят, х может быть рациональным если А.В.С.Д - рациональные числа ?
АШ
конечно, например A=B=C=D=0
CJ
по идее может. например, a, b = 1, c, d = 0. но могут быть случаи, когда подкоренное выражение меньше нуля, когда там получаются числа, из которых извлечение корня дает иррациональное число
АГ
Если рассмотреть случай когда все числа разные и не равны нулю и находятся в промежутке (0;корня из 2) ?
АГ
ну про промежуток не важно, главное не равны друг другу и нулю
ЛН
Что за фигнёй вы занимаетесь
У вас формула разности квадратов, она по определению раскладывается на множители A^2 - B^2 = (A-B)(A+B)
Дальше вам только так подобрать, чтобы произведение двух множителей давало точный квадрат
У вас формула разности квадратов, она по определению раскладывается на множители A^2 - B^2 = (A-B)(A+B)
Дальше вам только так подобрать, чтобы произведение двух множителей давало точный квадрат
АГ
а возможно ли такие подобрать ?
я считаю что невозможно
я считаю что невозможно
S
Хочу подарить своему племяннику 9-класнику книгу, чтоб начать врыв в геймдев, в частности, в юнити, он ходил на курсы по робототехнике полгода, поэтому уровень практически нулевой. Что взять?
S
ещё есть сайт, тип список шагов для вкатывания в разные сферы. забыл, как называется, подсобите плз
A
ну в нём проще всего вроде бы.
A
простейшее доказательство по индукции: сначала приводим одну строку и один столбец, по индукции добиваем остаток. это было в Алгебре Фаддеева, если не путаю.
там есть тонкий момент: бывает нужно взять полусумму и полуразность двух координат, например, для формы [0, 1; 1, 0]
там есть тонкий момент: бывает нужно взять полусумму и полуразность двух координат, например, для формы [0, 1; 1, 0]
A
это просто бред даунов, решивших поучить детей, но не знающих вообще ничего.
я бы поставил на "экспертов", но невозможно понять логику непрофессионала.
я бы поставил на "экспертов", но невозможно понять логику непрофессионала.
ET
Это же теорема Лагранжа для квадратичных форм. Доказательство в любом учебнике по линалу.
АД
Спасибо :D
ET
Не за что. ;)
АГ
можно ли как то доказать возможность нахождения рационального х если переменные рациональные , не равны нулю и не равны друг другу?
Разве ни кто не знает?
Разве ни кто не знает?
P
Товарищи. Кто электроникой занимается? Интересует где можно по дешёвке микросхем купить. Я просто не знаю.
ХШ
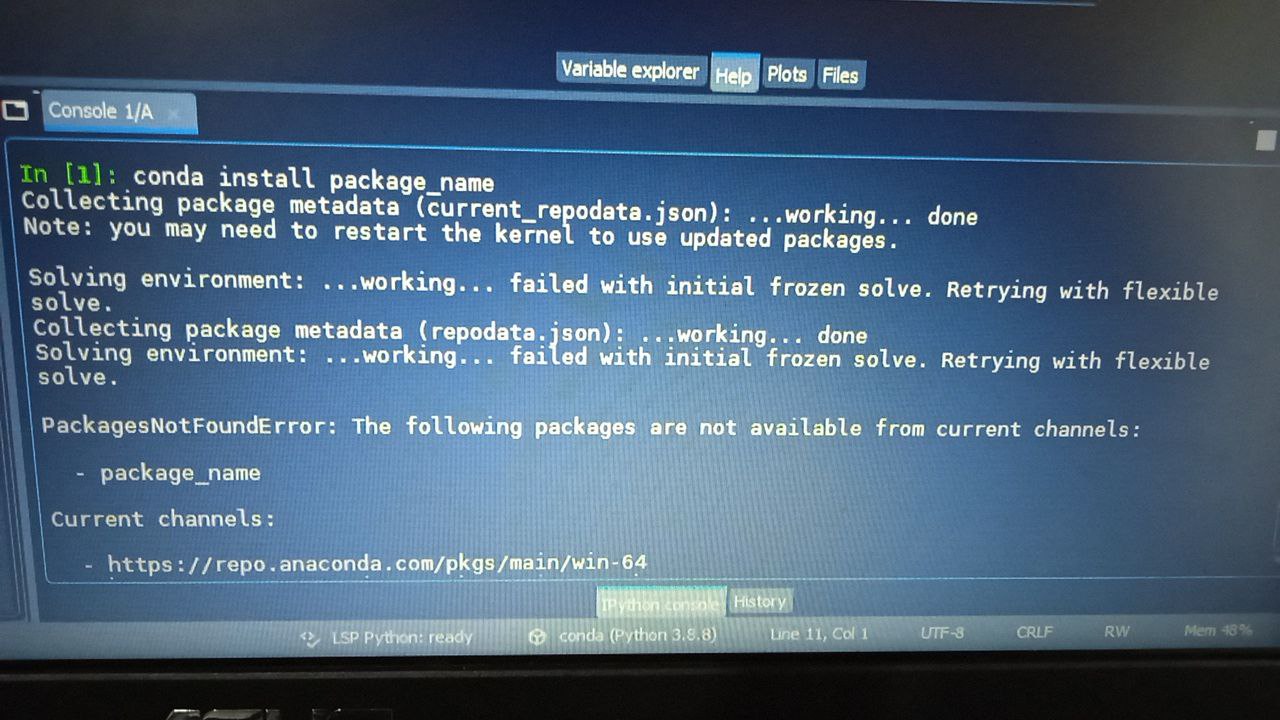
Ребята так обновляется Spyder(Python 3.8)
ЮК
conda install spyder



