Ну мы ж не знаем, по смыслу х - время, координата или что-то еще

А потом решать методом Эйлера для системы

НУ должны  быть в начале, а граничные  - на границе

Так стоп, а метод Эйлера - просто численное интегрирование что ли? 😂

Внезапно?)))

В начале координат или на границе времени?)

Ага😂так тогда же хоть самому можно вручную сделать

Я не разделяю время и не время.  Это в математике называется граничными условиями и начальными

Конечно! Составил систему для узлов и всё, и хорошо

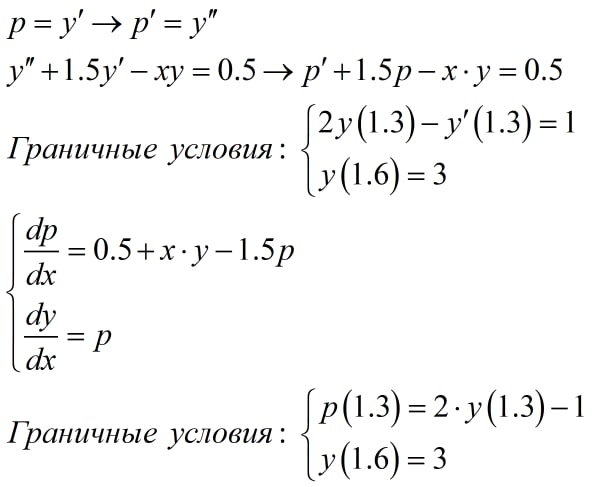
Проблема второго порядка решается заменой переменной. Далее можно попробовать решить численным методом Эйлера систему из двух ДУ 1-го порядка.   @Skyunder
Граничные условия 3-го рода и 1-го рода
Отрезок [1.3 ; 1.6]
Шаг разбиения h выбрать маленький.
Можно положить, что начальное значение производной y'(1.6)  = p(1.6) = L, где L - неизвестная величина. Её значение нужно найти так, чтобы выполнялось левое граничное условие. Выбрать два значения L = L1 и L = L2. Решить две задачи Коши для уравнения с НУ:
y(1.6) = 3   y'(1.6)  = p(1.6) = L1
y(1.6) = 3   y'(1.6)  = p(1.6) = L2
Полученные решения обозначить y1(x) и y2(x). Далее посчитать значения левых частей в ГУ на левой границе 2*y(1.3) - y'(1.3) = 1 для двух полученных функций  y1(x) и y2(x).
Получится:
2*y1(1.3) - y1'(1.3) = b1
2*y2(1.3) - y2'(1.3) = b2
b1 и b2 — c помощью численного решения Эйлера.
Далее искомое y'(1.6)  = p(1.6) = L найти с помощью линейной интерполяции.

Так, а вот это уже интересно

Или не про численное интегрироаание речь?

Ну подождите
Вот допустим ДУ на переменные x и t
И начальные условия y(x, t=0) = f(x), граничные y(x=0, t) = g1(t), y(x=l, t) = g2(t)

Я прост думал, тупо интегрируешь пошагово

А это неточно, так? Поэтому надо составить систему линейных уравнений и решить ее

Хм, теперь я стал лучше понимать ДУ

Можно достаточно абстрактно сказать, что после «начального» условия нас интересует эволюция, а в «граничных» – происходящее внутри границ/при определенных условиях на них

Можно представить себе струну

Струна закреплена в двух точках – это граничные условия

Мы отклоняем струну и отпускаем. Как именно мы её отклонили, прежде чем отпустить, это начальные условия