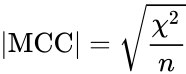K
Size: a a a
2019 August 26
Можно сравнить c TVöD, но вообще 50к(гросс) это вроде слегка выше средней по Германии, поэтому норм должно быть.
И вам тоже:)
ИК
Как заставить себя читать статьи, а не историю независимых батлов хипхоп ру?
SK
не заствляй, занимайся херне, главное потом не плакать
S
Как заставить себя читать статьи, а не историю независимых батлов хипхоп ру?
Ну вот, теперь нам читать что за независимые батлы хипхоп ру.
R
Как заставить себя читать статьи, а не историю независимых батлов хипхоп ру?
Они после 14 стали неинтересными в любом случае, дойдёшь до него и китайские предпринты на архиве покажутся лучшим времяпрепровождением.
R
Главное - после этого не отправиться читать статьи и комментарии с сайта "прайм крайм", там и контента больше и угара.
ИК
Так он в основном в официальных зажигал
LL
стоп стоп стоп
M
)
D[
стоп стоп стоп
Ругаться насяльника?
BK
дай угадаю - опять юзали ROC-кривые на несбалансированных выборках?!
ROC-кривые использовать на несбалансированных выборках - нормальная тема и не является суровой ошибкой. Они для этого и нужны, чтобы игнорировать дисбаланс. Проблема ROC-кривых в том, что они не различают классы по важности. ROC-кривые стоит использовать, если детекция обоих классов одинаково важна, просто так получилось, что у нас в выборке дисбаланс. Если же нас интересует детекция аномалий, то лучше, возможно, смотреть PR-кривые, но это на самом деле дело вкуса, потому что если модель доминирует в ROC-пространстве, то она доминирует и в PR (есть теорема). В целом, при отборе моделей, если классы разбалансированы, нужно считать не только ROC и PR, но и F1, сбалансированную точность и (альтернативный вариант специально для @leria_k) корреляцию Мэтьюза. И не использовать что-то одно из этого, потому что максимизация ROC-AUC не ведет к максимизации PR-AUC автоматически (и наоборот, и так далее). Статью подробно не читал, но скорее всего авторы накосячили в том, что посчитали, раз ROC-AUC большой, то модель автоматически имба, что не так.
SK
А вообще лучше репортить все метрики
SK
F1 тоже тоже надо аккруатно - какой порог, какая бетта, вот это все
SK
(а еще репортить данные от дамми класификаторов, чтобы а наши результы вообще лучше рандома)
BK
Вот да
BK
Дамми и бейслайн ето обязательно
H🐈
ROC-кривые использовать на несбалансированных выборках - нормальная тема и не является суровой ошибкой. Они для этого и нужны, чтобы игнорировать дисбаланс. Проблема ROC-кривых в том, что они не различают классы по важности. ROC-кривые стоит использовать, если детекция обоих классов одинаково важна, просто так получилось, что у нас в выборке дисбаланс. Если же нас интересует детекция аномалий, то лучше, возможно, смотреть PR-кривые, но это на самом деле дело вкуса, потому что если модель доминирует в ROC-пространстве, то она доминирует и в PR (есть теорема). В целом, при отборе моделей, если классы разбалансированы, нужно считать не только ROC и PR, но и F1, сбалансированную точность и (альтернативный вариант специально для @leria_k) корреляцию Мэтьюза. И не использовать что-то одно из этого, потому что максимизация ROC-AUC не ведет к максимизации PR-AUC автоматически (и наоборот, и так далее). Статью подробно не читал, но скорее всего авторы накосячили в том, что посчитали, раз ROC-AUC большой, то модель автоматически имба, что не так.
кстати, про "классы по важности" — а как работать с классами, где ошибки неравноценны? (вот этот весь "cost-sensitive-classification")
через максимизацию PR-AUC ?
через максимизацию PR-AUC ?
AP
ROC-кривые использовать на несбалансированных выборках - нормальная тема и не является суровой ошибкой. Они для этого и нужны, чтобы игнорировать дисбаланс. Проблема ROC-кривых в том, что они не различают классы по важности. ROC-кривые стоит использовать, если детекция обоих классов одинаково важна, просто так получилось, что у нас в выборке дисбаланс. Если же нас интересует детекция аномалий, то лучше, возможно, смотреть PR-кривые, но это на самом деле дело вкуса, потому что если модель доминирует в ROC-пространстве, то она доминирует и в PR (есть теорема). В целом, при отборе моделей, если классы разбалансированы, нужно считать не только ROC и PR, но и F1, сбалансированную точность и (альтернативный вариант специально для @leria_k) корреляцию Мэтьюза. И не использовать что-то одно из этого, потому что максимизация ROC-AUC не ведет к максимизации PR-AUC автоматически (и наоборот, и так далее). Статью подробно не читал, но скорее всего авторы накосячили в том, что посчитали, раз ROC-AUC большой, то модель автоматически имба, что не так.
Ну да, разумно. В бложике который я выше привел это и написано, в общем. Понятно что в работе где смертность исследуют, ценность классов сурово неодинакова.
BK
кстати, про "классы по важности" — а как работать с классами, где ошибки неравноценны? (вот этот весь "cost-sensitive-classification")
через максимизацию PR-AUC ?
через максимизацию PR-AUC ?
Типа да, мцц тож попробуй. Так-то если у тебя набор моделей, можешь их и по roc отобрать
H🐈
Типа да, мцц тож попробуй. Так-то если у тебя набор моделей, можешь их и по roc отобрать
а что такое мцц?
вот это, что ли — https://en.wikipedia.org/wiki/Matthews_correlation_coefficient ???
вот это, что ли — https://en.wikipedia.org/wiki/Matthews_correlation_coefficient ???