AD
Size: a a a
2020 May 01
основной поток фивт
AD
а домашку легально спрашивать?
DK
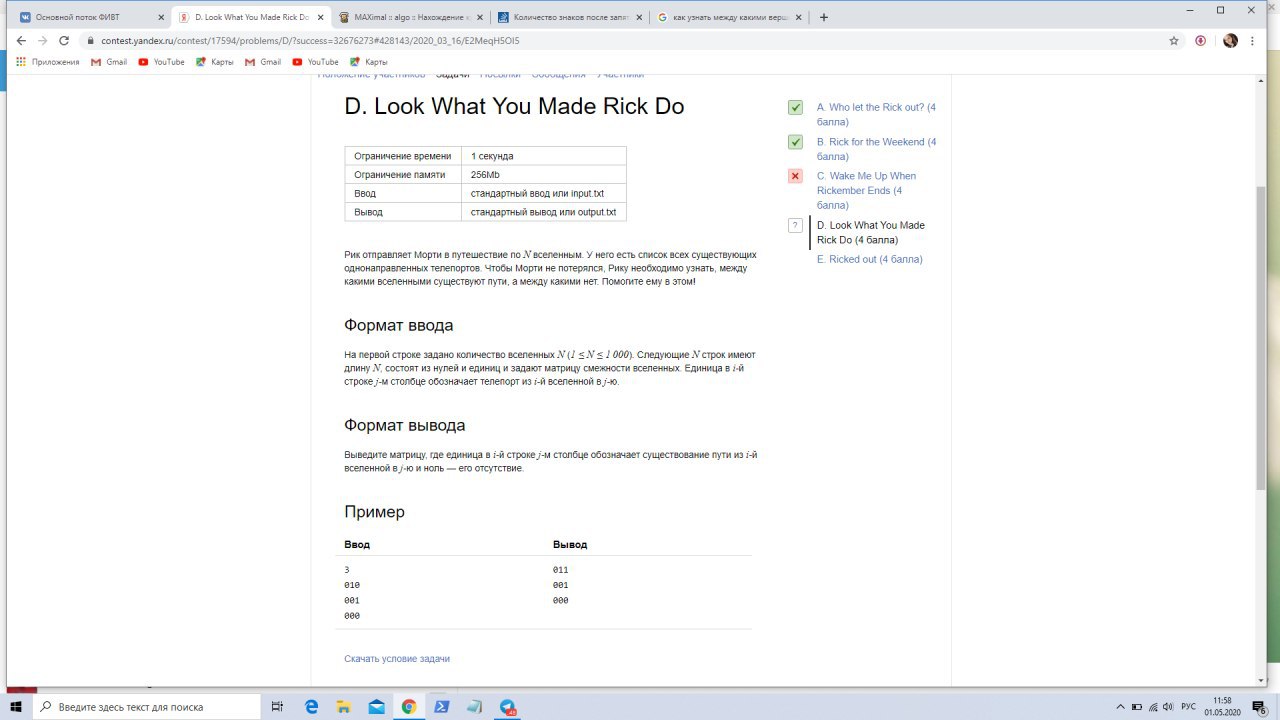
Можно найти компоненты сильной связности. Это делается за O(n^2). Их будет не больше тысячи.
Внутри каждой компоненты между любыми двумя вершинами будет путь.
Граф из компонент сильной связности будет ациклическим.
Из вершин в одной компоненте есть пути во всех ее потомков в других компонентах. Обратно - нет.
Так как компонент будет не более 1000, то ациклическую часть можно решать за квадрат.
Итого O(N^2)
Внутри каждой компоненты между любыми двумя вершинами будет путь.
Граф из компонент сильной связности будет ациклическим.
Из вершин в одной компоненте есть пути во всех ее потомков в других компонентах. Обратно - нет.
Так как компонент будет не более 1000, то ациклическую часть можно решать за квадрат.
Итого O(N^2)
EZ
Выдал ро на недельку, решай дз сам(а)
ПК
Правда ли, что произведение всех делителей числа n — O(n log n)?
ПК
зачем тут дейкстра бтв?
ПК
там же дикая асимптотика с дейкстрой будет
ПК
между
nm log n и n³ вродеMB
Правда ли, что произведение всех делителей числа n — O(n log n)?
sqrt(N) ** d(n)
ПК
Правда ли, что произведение всех делителей числа n — O(n log n)?
А, ну очевидно да
ПК
Т.к. сумма гармонического ряда O(log n)
EZ
Правда ли, что произведение всех делителей числа n — O(n log n)?
2^n?
MB
А, ну очевидно да
Всмысле? Если у числа хотя бы 2 пары делителей, то уже n*n
ПК
Всмысле? Если у числа хотя бы 2 пары делителей, то уже n*n
хм
ПК
ну ок
KK
Правда ли, что произведение всех делителей числа n — O(n log n)?
Сумма O(n ^ (4/3))
ПК
да, я ошибся, спасибо
ПК
я понял, сумма O(n log n) точно, а произведение может быть очень большим
ПК
Сумма O(n ^ (4/3))
А откуда такая оценка?
MB
я понял, сумма O(n log n) точно, а произведение может быть очень большим
Почему сумма O(n log n)?