А вот в случае если матрица вырождена разложение не единственно

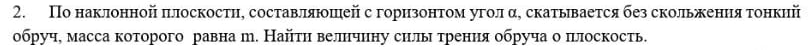
Скажите пожалуйста,я правильно решил эту задачу или нет

Кто-нибудь посмотрите пожалуйста

Да,но я не представляю ,как найти хотя бы одно из разложений

А можете показать матрицу AA* ?

Вы неправильно интерпретируете. Нет никаких переходов. Есть преобразование плоскости

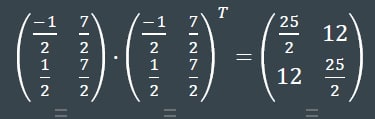
(умножаю на транспонированную, поскольку в ортонормированном матрица сопряженного равна транспонированной матрице исходного)

Окей. Мне кажется  тут надо смотреть как поворот изометрию и растяжение по осям, чтобы найти разложение

Собственно когда будете обдумывать  этом метод, поймете почему разложение не единсивенно

То есть, мне надо рассмотреть оператор A как некоторое преобразование плоскости (в данном случае), в этом преобразовании увидеть геометрическую составляющую какого-то преобразования плоскости , которое имеет ортогональную матрицу и какого-то преобразования плоскости с симметричной матрицей

Да

окей, подумаю,спасибо

Насчет роли симметричного преобразования надо подумать

как раз будет повод увидеть геометрическую составляющую линала

Очень важная штука

Конкретно в этой задаче ответ почти очевиден из геометрии

Кстати , с матрицами налажал ,в первой строке минус потерял. Что касательно геометрического смысла оператора А: получилось заметить,что базисные векторы переносятся на биссектрису второй четверти,значит и все векторы с плоскости перейдут на биссектрису второй/четвертой четвертей. Про смысл преобразований: ортогональный сохраняет расстояние между точками плоскости , как-то точки сдвигает ,но расстояния не меняет (ну или же длину векторов) ,симметричное же растягивает по осям ( в зависимости от того ,что на диагонали ). На плоскости с сохранением расстояний мы можем вроде повернуть вокруг точки и сдвинуть на какой-то вектор, растяжение ж понятно что творит. Дурацкий вопрос: как в результате таких преобразований мы получили перенос всех векторов плоскости на одну прямую

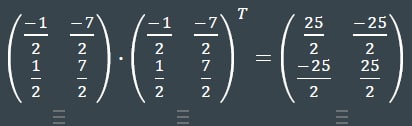
Уже точно правильные матрицы

А вы подумайте какие преобразования являются изометриями и какие преоьразования описываются симметричными матрицами