L
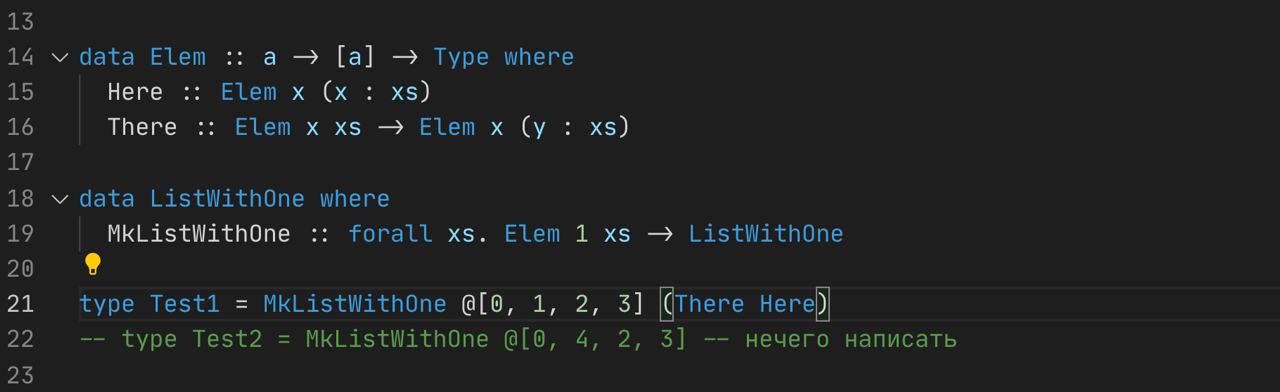
data Test
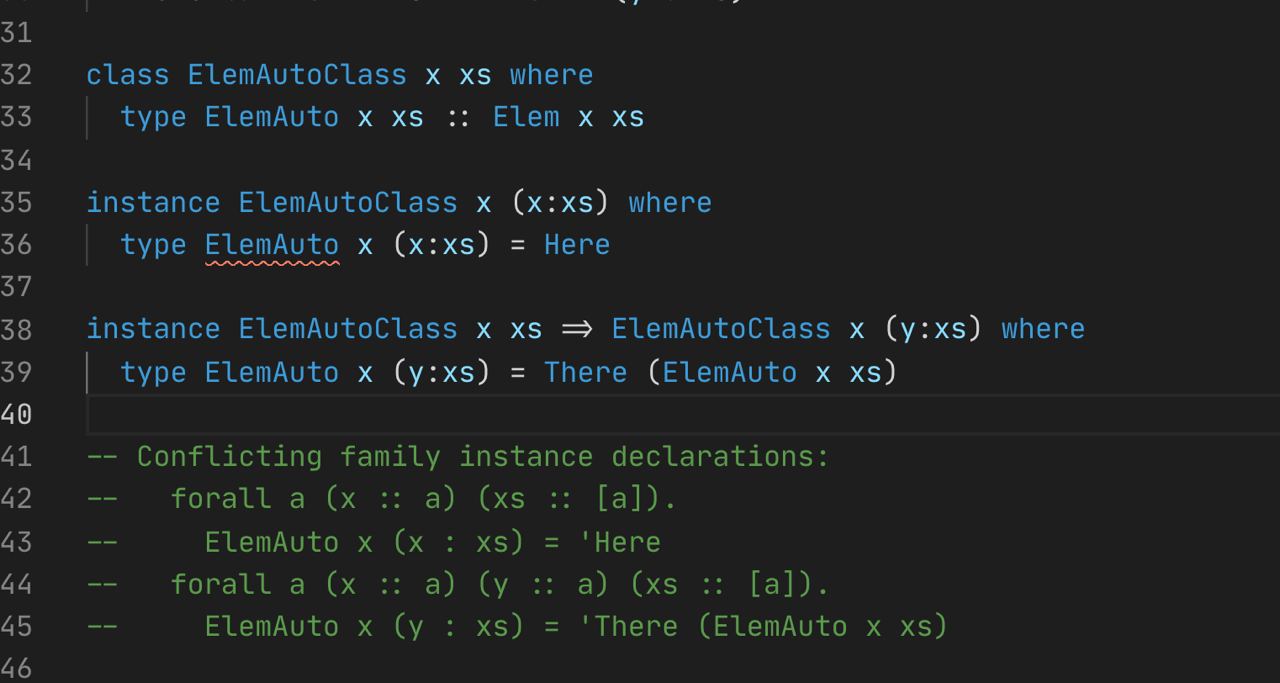
class SomeClass (a :: Type)
class (forall a. SomeClass a) => Cls a
instance SomeClass Test
instance Cls Test
Получаем No instance for (SomeClass a) в последней строчке, что вполне ожидаемо при обычных правилах области видимости для forall. Если переименовать class (forall a. SomeClass a) => Cls b эффект такой же, что тоже ожидаемо. Это разные переменные.