к
Size: a a a
2021 March 31
AA
Всё ещё не понимаю, как на типа-зависимом хаскеле ввести с консольки число
n, а затем вектор длины nзависимого хаскеля в смысле зависимых типов в хаскеле нет, есть завкайнды
для того шоб это делать завтипы не нужны, нужны экзистенциальные типы
делается это примерно как везде, сконструировать док-во по тому что вводится что введенное число и введенный список длинны равной этому числу
после этого паттерматчнуть док-во и в ветке паттернматча будут типы какие надо
отличаться от языка с завтипами нормального это будет
1) убогими континуэйшон лесенками из-за убогих экзистенциальных типов в хаскеле
2) дублированием кода, потому что в отличие от языка с завтипами каждую функцию надо писать три раза, для значений для типов и для синглетонов
для того шоб это делать завтипы не нужны, нужны экзистенциальные типы
делается это примерно как везде, сконструировать док-во по тому что вводится что введенное число и введенный список длинны равной этому числу
после этого паттерматчнуть док-во и в ветке паттернматча будут типы какие надо
отличаться от языка с завтипами нормального это будет
1) убогими континуэйшон лесенками из-за убогих экзистенциальных типов в хаскеле
2) дублированием кода, потому что в отличие от языка с завтипами каждую функцию надо писать три раза, для значений для типов и для синглетонов
NI
зависимого хаскеля в смысле зависимых типов в хаскеле нет, есть завкайнды
для того шоб это делать завтипы не нужны, нужны экзистенциальные типы
делается это примерно как везде, сконструировать док-во по тому что вводится что введенное число и введенный список длинны равной этому числу
после этого паттерматчнуть док-во и в ветке паттернматча будут типы какие надо
отличаться от языка с завтипами нормального это будет
1) убогими континуэйшон лесенками из-за убогих экзистенциальных типов в хаскеле
2) дублированием кода, потому что в отличие от языка с завтипами каждую функцию надо писать три раза, для значений для типов и для синглетонов
для того шоб это делать завтипы не нужны, нужны экзистенциальные типы
делается это примерно как везде, сконструировать док-во по тому что вводится что введенное число и введенный список длинны равной этому числу
после этого паттерматчнуть док-во и в ветке паттернматча будут типы какие надо
отличаться от языка с завтипами нормального это будет
1) убогими континуэйшон лесенками из-за убогих экзистенциальных типов в хаскеле
2) дублированием кода, потому что в отличие от языка с завтипами каждую функцию надо писать три раза, для значений для типов и для синглетонов
Ну уж какое-то подобие universe-полиморфизма придумают уж...
Y
зависимого хаскеля в смысле зависимых типов в хаскеле нет, есть завкайнды
для того шоб это делать завтипы не нужны, нужны экзистенциальные типы
делается это примерно как везде, сконструировать док-во по тому что вводится что введенное число и введенный список длинны равной этому числу
после этого паттерматчнуть док-во и в ветке паттернматча будут типы какие надо
отличаться от языка с завтипами нормального это будет
1) убогими континуэйшон лесенками из-за убогих экзистенциальных типов в хаскеле
2) дублированием кода, потому что в отличие от языка с завтипами каждую функцию надо писать три раза, для значений для типов и для синглетонов
для того шоб это делать завтипы не нужны, нужны экзистенциальные типы
делается это примерно как везде, сконструировать док-во по тому что вводится что введенное число и введенный список длинны равной этому числу
после этого паттерматчнуть док-во и в ветке паттернматча будут типы какие надо
отличаться от языка с завтипами нормального это будет
1) убогими континуэйшон лесенками из-за убогих экзистенциальных типов в хаскеле
2) дублированием кода, потому что в отличие от языка с завтипами каждую функцию надо писать три раза, для значений для типов и для синглетонов
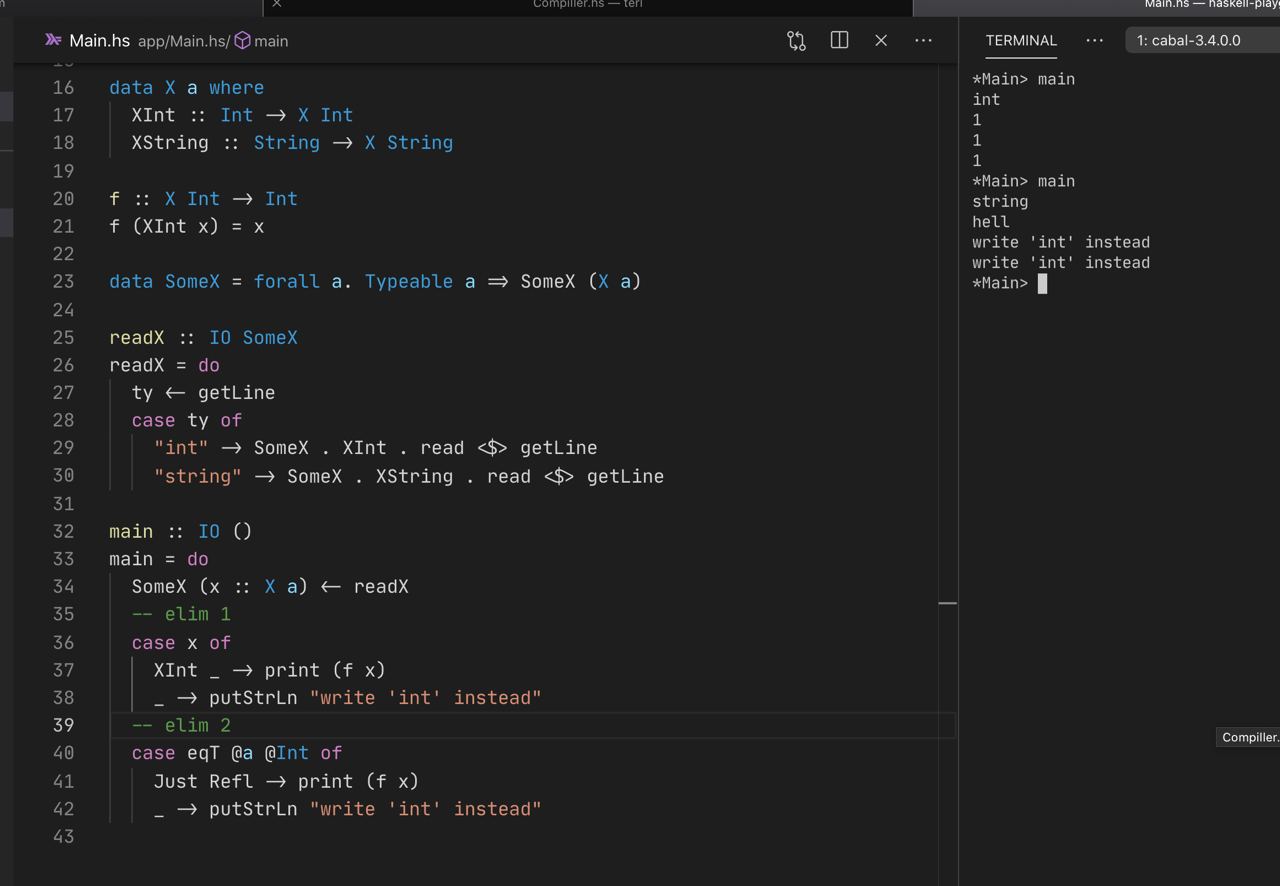
Мне бы код бы…
AA
Мне бы код бы…
{-# LANGUAGE PolyKinds, DataKinds, TypeFamilies, GADTs #-}
{-# LANGUAGE TypeOperators, NPlusKPatterns #-}
{-# LANGUAGE DeriveFoldable, StandaloneDeriving, TypeApplications #-}
{-# LANGUAGE TemplateHaskell #-}
import Data.Singletons
import Data.Singletons.TH
import Text.Read (readMaybe)
import Data.Kind (Type)
import qualified Data.Foldable as F
data Nat = Z | S Nat deriving Show
intToNat 0 = Z
intToNat (n + 1) = S (intToNat n)
genSingletons [''Nat]
-- генерирует синглетоны для Nat:
-- data instance Sing (n :: Nat) where
-- SZ :: Sing Z
-- SS :: Sing n -> Sing (S n)
-- instance SingKind Nat where
-- type DemoteRep Nat = Nat
-- fromSing SZ = Z
-- fromSing (SS b) = S (fromSing b)
-- toSing Z = SomeSing SZ
-- toSing (S b) = case toSing b :: SomeSing Nat of
-- SomeSing c -> SomeSing (SS c)
data Vect :: Nat -> Type -> Type where
V0 :: Vect Z x
(:>) :: x -> Vect n x -> Vect (S n) x
deriving instance Foldable (Vect n)
infixr 5 :>
getInt :: IO Int
getInt = do
resp <- getLine
case readMaybe @Int resp of
Just value -> pure value
Nothing -> do
putStrLn "error"
getInt
makeVect :: Sing (size :: Nat) -> a -> Vect size a
makeVect SZ _ = V0
makeVect (SS x) v = v :> makeVect x v
zipVect :: Vect size a -> Vect size b -> Vect size (a, b)
zipVect V0 V0 = V0
zipVect (x1 :> v1) (x2 :> v2) = (x1, x2) :> zipVect v1 v2
main :: IO ()
main = do
putStrLn "Hello world"
size <- getInt
-- нету "голых" экзистенциальных типов,
-- работать с синглетоном числа придется только в континьюэйшене
withSomeSing (intToNat size) $ \ssize -> do
let vect1 = makeVect ssize size
let vect2 = makeVect ssize "^_^"
-- let vect2 = makeVect (SS ssize) "^_^" -- вызовет ошибку
print . F.toList $ vect1
print . F.toList $ vect2
print . F.toList $ zipVect vect1 vect2L
зависимого хаскеля в смысле зависимых типов в хаскеле нет, есть завкайнды
для того шоб это делать завтипы не нужны, нужны экзистенциальные типы
делается это примерно как везде, сконструировать док-во по тому что вводится что введенное число и введенный список длинны равной этому числу
после этого паттерматчнуть док-во и в ветке паттернматча будут типы какие надо
отличаться от языка с завтипами нормального это будет
1) убогими континуэйшон лесенками из-за убогих экзистенциальных типов в хаскеле
2) дублированием кода, потому что в отличие от языка с завтипами каждую функцию надо писать три раза, для значений для типов и для синглетонов
для того шоб это делать завтипы не нужны, нужны экзистенциальные типы
делается это примерно как везде, сконструировать док-во по тому что вводится что введенное число и введенный список длинны равной этому числу
после этого паттерматчнуть док-во и в ветке паттернматча будут типы какие надо
отличаться от языка с завтипами нормального это будет
1) убогими континуэйшон лесенками из-за убогих экзистенциальных типов в хаскеле
2) дублированием кода, потому что в отличие от языка с завтипами каждую функцию надо писать три раза, для значений для типов и для синглетонов
Киньте что ли ссылкой какой где про эти Ваши завкайнды что-нибудь написано. Я по ходу не в теме, гугл молчит как рыба об лёд.
AA
Киньте что ли ссылкой какой где про эти Ваши завкайнды что-нибудь написано. Я по ходу не в теме, гугл молчит как рыба об лёд.
ну вон выше кана написал же
AA
Мне бы код бы…
это не в точности то что требовалось, а даже сложнее, думаю понятно как это переписать чтоб было в точности то
IR
да, я использовал недавно bnfc-meta (https://github.com/ulysses4ever/BNFC-meta/blob/master/examples/typesafe/Typesafe.hs), он тоже template haskell-ем генерирует CST
оно умеет в нормальные сообщения об ошибках лексера/парсера или как обычно для алекса/хэппи взрыв на ascii-фабрике?
IR
эх...