I
Size: a a a
2020 May 24
Вопрос звучал по другому
яж вроде невам писал
P
И что
RG
Добрый день, Коллеги.
Вопрос по опыту поиска минимума функции.
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import minimize_scalar, minimize
from sklearn.metrics import f1_score
%matplotlib inline
actual_11 = np.array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
predicted_11 = np.array([ 0.35929566, 0.61562123, 0.71974688, 0.24893298, 0.19056711, 0.89308488,
0.71155538, 0.00903258, 0.51950535, 0.72153302, 0.45936068, 0.20197229, 0.67092724,
0.81111343, 0.65359427, 0.70044585, 0.61983513, 0.84716577, 0.8512387 ,
0.86023125, 0.7659328 , 0.70362246, 0.70127618, 0.8578749 , 0.83641841,
0.62959491, 0.90445368])
def f1_score_minimizeT(k, actual, predicted):
return -abs(f1_score(actual, predicted>0.1*k))
res = minimize_scalar(f1_score_minimizeT, args=(actual_11, predicted_11), bounds=(3,7), method='bounded', options={'disp':3})
linspace = np.linspace(0, 10, 100)
plt.plot(linspace, [f1_score(actual_11, predicted_11>0.1*x) for x in linspace], label="f1")
plt.plot(linspace, [f1_score_minimizeT(x, actual_11, predicted_11) for x in linspace], label="f1_minimize_model")
plt.plot([res.x, res.x], [-1, 1], label="best")
Вывод результата поиска минимума функции:
Func-count x f(x) Procedure
1 4.52786 -0.742857 initial
2 5.47214 -0.787879 golden
3 6.05573 -0.787879 golden
4 5.76393 -0.787879 parabolic
5 5.65248 -0.787879 golden
6 5.58359 -0.787879 golden
7 5.54102 -0.787879 golden
8 5.51471 -0.787879 golden
9 5.49845 -0.787879 golden
10 5.4884 -0.787879 golden
11 5.48219 -0.787879 golden
12 5.47835 -0.787879 golden
13 5.47597 -0.787879 golden
14 5.47451 -0.787879 golden
15 5.4736 -0.787879 golden
16 5.47304 -0.787879 golden
17 5.4727 -0.787879 golden
18 5.47248 -0.787879 golden
19 5.47235 -0.787879 golden
20 5.47227 -0.787879 golden
21 5.47222 -0.787879 golden
22 5.47219 -0.787879 golden
23 5.47217 -0.787879 golden
24 5.47216 -0.787879 golden
25 5.47215 -0.787879 golden
26 5.47214 -0.787879 golden
27 5.47214 -0.787879 golden
На графике сверху изображено f1_score для оценки, а снизу изображена перевернутая функция, чтобы найти минимум этой функции. И видно, что выбор минимального значения сделан не совсем точно.
Вопрос, как сообщить функции minimize_scalar выполнять большее число шагов для поиска минимума. Или возможно для подобных графиков поиск минимума выполняется по-другому?
Вопрос по опыту поиска минимума функции.
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import minimize_scalar, minimize
from sklearn.metrics import f1_score
%matplotlib inline
actual_11 = np.array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
predicted_11 = np.array([ 0.35929566, 0.61562123, 0.71974688, 0.24893298, 0.19056711, 0.89308488,
0.71155538, 0.00903258, 0.51950535, 0.72153302, 0.45936068, 0.20197229, 0.67092724,
0.81111343, 0.65359427, 0.70044585, 0.61983513, 0.84716577, 0.8512387 ,
0.86023125, 0.7659328 , 0.70362246, 0.70127618, 0.8578749 , 0.83641841,
0.62959491, 0.90445368])
def f1_score_minimizeT(k, actual, predicted):
return -abs(f1_score(actual, predicted>0.1*k))
res = minimize_scalar(f1_score_minimizeT, args=(actual_11, predicted_11), bounds=(3,7), method='bounded', options={'disp':3})
linspace = np.linspace(0, 10, 100)
plt.plot(linspace, [f1_score(actual_11, predicted_11>0.1*x) for x in linspace], label="f1")
plt.plot(linspace, [f1_score_minimizeT(x, actual_11, predicted_11) for x in linspace], label="f1_minimize_model")
plt.plot([res.x, res.x], [-1, 1], label="best")
Вывод результата поиска минимума функции:
Func-count x f(x) Procedure
1 4.52786 -0.742857 initial
2 5.47214 -0.787879 golden
3 6.05573 -0.787879 golden
4 5.76393 -0.787879 parabolic
5 5.65248 -0.787879 golden
6 5.58359 -0.787879 golden
7 5.54102 -0.787879 golden
8 5.51471 -0.787879 golden
9 5.49845 -0.787879 golden
10 5.4884 -0.787879 golden
11 5.48219 -0.787879 golden
12 5.47835 -0.787879 golden
13 5.47597 -0.787879 golden
14 5.47451 -0.787879 golden
15 5.4736 -0.787879 golden
16 5.47304 -0.787879 golden
17 5.4727 -0.787879 golden
18 5.47248 -0.787879 golden
19 5.47235 -0.787879 golden
20 5.47227 -0.787879 golden
21 5.47222 -0.787879 golden
22 5.47219 -0.787879 golden
23 5.47217 -0.787879 golden
24 5.47216 -0.787879 golden
25 5.47215 -0.787879 golden
26 5.47214 -0.787879 golden
27 5.47214 -0.787879 golden
На графике сверху изображено f1_score для оценки, а снизу изображена перевернутая функция, чтобы найти минимум этой функции. И видно, что выбор минимального значения сделан не совсем точно.
Вопрос, как сообщить функции minimize_scalar выполнять большее число шагов для поиска минимума. Или возможно для подобных графиков поиск минимума выполняется по-другому?
RG
P
Roman Gamanetc
Добрый день, Коллеги.
Вопрос по опыту поиска минимума функции.
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import minimize_scalar, minimize
from sklearn.metrics import f1_score
%matplotlib inline
actual_11 = np.array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
predicted_11 = np.array([ 0.35929566, 0.61562123, 0.71974688, 0.24893298, 0.19056711, 0.89308488,
0.71155538, 0.00903258, 0.51950535, 0.72153302, 0.45936068, 0.20197229, 0.67092724,
0.81111343, 0.65359427, 0.70044585, 0.61983513, 0.84716577, 0.8512387 ,
0.86023125, 0.7659328 , 0.70362246, 0.70127618, 0.8578749 , 0.83641841,
0.62959491, 0.90445368])
def f1_score_minimizeT(k, actual, predicted):
return -abs(f1_score(actual, predicted>0.1*k))
res = minimize_scalar(f1_score_minimizeT, args=(actual_11, predicted_11), bounds=(3,7), method='bounded', options={'disp':3})
linspace = np.linspace(0, 10, 100)
plt.plot(linspace, [f1_score(actual_11, predicted_11>0.1*x) for x in linspace], label="f1")
plt.plot(linspace, [f1_score_minimizeT(x, actual_11, predicted_11) for x in linspace], label="f1_minimize_model")
plt.plot([res.x, res.x], [-1, 1], label="best")
Вывод результата поиска минимума функции:
Func-count x f(x) Procedure
1 4.52786 -0.742857 initial
2 5.47214 -0.787879 golden
3 6.05573 -0.787879 golden
4 5.76393 -0.787879 parabolic
5 5.65248 -0.787879 golden
6 5.58359 -0.787879 golden
7 5.54102 -0.787879 golden
8 5.51471 -0.787879 golden
9 5.49845 -0.787879 golden
10 5.4884 -0.787879 golden
11 5.48219 -0.787879 golden
12 5.47835 -0.787879 golden
13 5.47597 -0.787879 golden
14 5.47451 -0.787879 golden
15 5.4736 -0.787879 golden
16 5.47304 -0.787879 golden
17 5.4727 -0.787879 golden
18 5.47248 -0.787879 golden
19 5.47235 -0.787879 golden
20 5.47227 -0.787879 golden
21 5.47222 -0.787879 golden
22 5.47219 -0.787879 golden
23 5.47217 -0.787879 golden
24 5.47216 -0.787879 golden
25 5.47215 -0.787879 golden
26 5.47214 -0.787879 golden
27 5.47214 -0.787879 golden
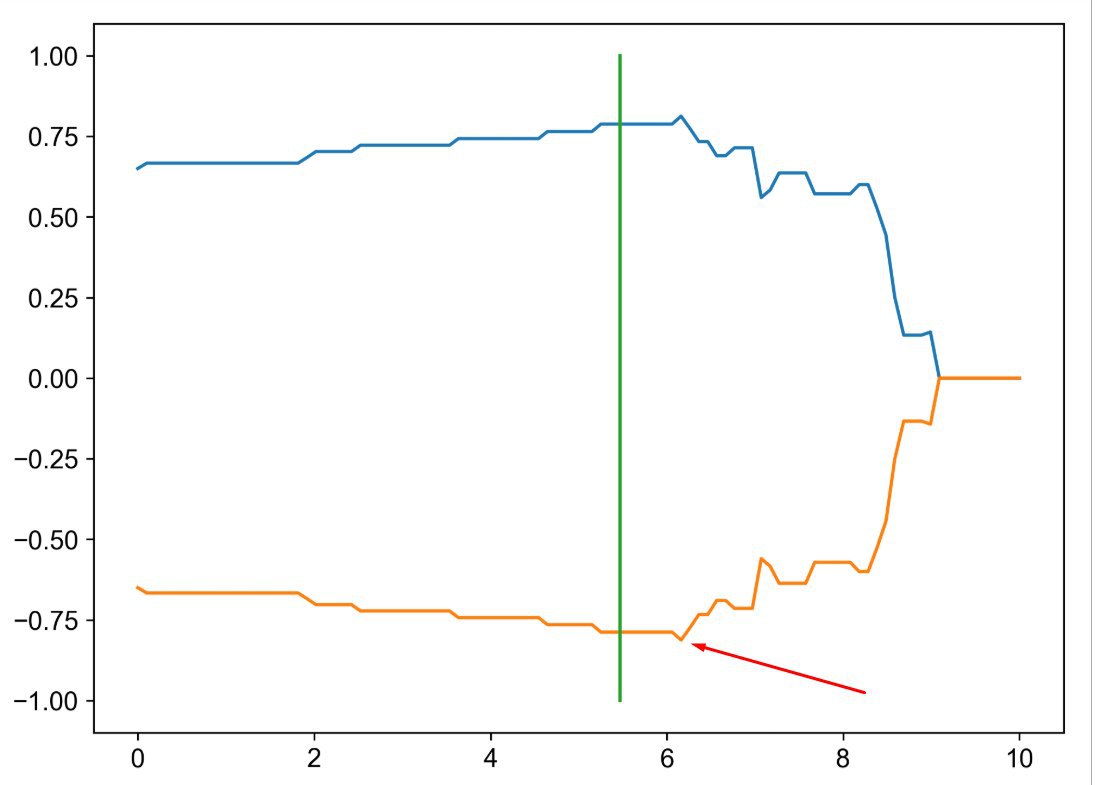
На графике сверху изображено f1_score для оценки, а снизу изображена перевернутая функция, чтобы найти минимум этой функции. И видно, что выбор минимального значения сделан не совсем точно.
Вопрос, как сообщить функции minimize_scalar выполнять большее число шагов для поиска минимума. Или возможно для подобных графиков поиск минимума выполняется по-другому?
Вопрос по опыту поиска минимума функции.
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import minimize_scalar, minimize
from sklearn.metrics import f1_score
%matplotlib inline
actual_11 = np.array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
predicted_11 = np.array([ 0.35929566, 0.61562123, 0.71974688, 0.24893298, 0.19056711, 0.89308488,
0.71155538, 0.00903258, 0.51950535, 0.72153302, 0.45936068, 0.20197229, 0.67092724,
0.81111343, 0.65359427, 0.70044585, 0.61983513, 0.84716577, 0.8512387 ,
0.86023125, 0.7659328 , 0.70362246, 0.70127618, 0.8578749 , 0.83641841,
0.62959491, 0.90445368])
def f1_score_minimizeT(k, actual, predicted):
return -abs(f1_score(actual, predicted>0.1*k))
res = minimize_scalar(f1_score_minimizeT, args=(actual_11, predicted_11), bounds=(3,7), method='bounded', options={'disp':3})
linspace = np.linspace(0, 10, 100)
plt.plot(linspace, [f1_score(actual_11, predicted_11>0.1*x) for x in linspace], label="f1")
plt.plot(linspace, [f1_score_minimizeT(x, actual_11, predicted_11) for x in linspace], label="f1_minimize_model")
plt.plot([res.x, res.x], [-1, 1], label="best")
Вывод результата поиска минимума функции:
Func-count x f(x) Procedure
1 4.52786 -0.742857 initial
2 5.47214 -0.787879 golden
3 6.05573 -0.787879 golden
4 5.76393 -0.787879 parabolic
5 5.65248 -0.787879 golden
6 5.58359 -0.787879 golden
7 5.54102 -0.787879 golden
8 5.51471 -0.787879 golden
9 5.49845 -0.787879 golden
10 5.4884 -0.787879 golden
11 5.48219 -0.787879 golden
12 5.47835 -0.787879 golden
13 5.47597 -0.787879 golden
14 5.47451 -0.787879 golden
15 5.4736 -0.787879 golden
16 5.47304 -0.787879 golden
17 5.4727 -0.787879 golden
18 5.47248 -0.787879 golden
19 5.47235 -0.787879 golden
20 5.47227 -0.787879 golden
21 5.47222 -0.787879 golden
22 5.47219 -0.787879 golden
23 5.47217 -0.787879 golden
24 5.47216 -0.787879 golden
25 5.47215 -0.787879 golden
26 5.47214 -0.787879 golden
27 5.47214 -0.787879 golden
На графике сверху изображено f1_score для оценки, а снизу изображена перевернутая функция, чтобы найти минимум этой функции. И видно, что выбор минимального значения сделан не совсем точно.
Вопрос, как сообщить функции minimize_scalar выполнять большее число шагов для поиска минимума. Или возможно для подобных графиков поиск минимума выполняется по-другому?
Ну вы наткнулись на участок функции с практически нулевым градиентом, это вероятно является условием остановки алгоритма. У параметров метода нашёл только максимальное количество итераций
P
Возможно стоит воспользоваться более ресурсоемким алгоритмом
V
спасиб ребят. тоже думал ток про признаки а не веса до сего разговора)😳
Вот и я нашел пример полезным)) до него, я думал только про признаки)
V
Привет. Спасибо за отзыв.
Если говорить про линейные модели: они линейны по параметрам и по (итоговым) признакам
Если говорить про линейные модели: они линейны по параметрам и по (итоговым) признакам
V
т.е представимы в виде линейной комбинации \sum_{i} (w_i * x_i)
V
в приведенном примере есть член w_i * w_j, т.е. модель уже нелинейна по параметрам
V
Если говорить про эту модель, то она линейна по преобразованным признакам (в которые вошел и x^2), и нелинейна по исходным
V
Это комментарий от Р.Нейчева по тому скрину) я еще до этого чата у него спросил тоже самое)
AO
Вот и я нашел пример полезным)) до него, я думал только про признаки)
Я до прост даже не задумывался:))
V
Специализация от вашингтонского универа классная, рекомендую)) там даже математика есть))
AO
Специализация от вашингтонского универа классная, рекомендую)) там даже математика есть))
я пока глубокое обучени взял на степике) и спикер знакомый))
V
я пока глубокое обучени взял на степике) и спикер знакомый))
Это какое?)
VN
Специализация от вашингтонского универа классная, рекомендую)) там даже математика есть))
А что за специализация?
AO
Это какое?)
Продвинутое что то там) там Радослав один из спикеров
V
а, ну это deep learning school




