Size: a a a
2019 March 18

2019 March 19

Доброго времени суток, канал как и любой проект планирует развиваться. Собственно я хотел бы открыть информационный портал. В скором времени, свое свободное время буду отдавать на него. Конечно буду делать на Django. Собираю деньги на аренду хостинга😁
Если есть тот кто желает поддержать проект, вот реквизиты:
MasterCard
5599005004199621
Если есть тот кто желает поддержать проект, вот реквизиты:
MasterCard
5599005004199621
2019 March 20

Регуля́рные выраже́ния (англ. regular expressions) — формальный язык поиска и осуществления манипуляций с подстроками в тексте, основанный на использовании метасимволов (символов-джокеров, англ. wildcard characters). Для поиска используется строка-образец (англ. pattern, по-русски её часто называют «шаблоном», «маской»), состоящая из символов и метасимволов и задающая правило поиска. Для манипуляций с текстом дополнительно задаётся строка замены, которая также может содержать в себе специальные символы.
https://tproger.ru/translations/regular-expression-python/amp/
https://tproger.ru/translations/regular-expression-python/amp/
2019 March 21

Результатом работы с регулярным выражением может быть:
проверка наличия искомого образца в заданном тексте;
определение подстроки текста, которая сопоставляется образцу;
определение групп символов, соответствующих отдельным частям образца.
Если регулярное выражение используется для замены текста, то результатом работы будет новая текстовая строка, представляющая из себя исходный текст, из которого удалены найденные подстроки (сопоставленные образцу), а вместо них подставлены строки замены (возможно, модифицированные запомненными при разборе группами символов из исходного текста). Частным случаем модификации текста является удаление всех вхождений найденного образца — для чего строка замены указывается пустой.
проверка наличия искомого образца в заданном тексте;
определение подстроки текста, которая сопоставляется образцу;
определение групп символов, соответствующих отдельным частям образца.
Если регулярное выражение используется для замены текста, то результатом работы будет новая текстовая строка, представляющая из себя исходный текст, из которого удалены найденные подстроки (сопоставленные образцу), а вместо них подставлены строки замены (возможно, модифицированные запомненными при разборе группами символов из исходного текста). Частным случаем модификации текста является удаление всех вхождений найденного образца — для чего строка замены указывается пустой.

Истоки регулярных выражений лежат в теории автоматов, теории формальных языков и классификации формальных грамматик по Хомскому.
Эти области изучают вычислительные модели (автоматы) и способы описания и
классификации формальных языков. В 1940-х гг. Уоррен Маккалок и Уолтер Питтс описали нейронную систему, используя простой автомат в качестве модели нейрона.
Математик Стивен Клини позже описал эти модели, используя свою систему математических обозначений, названную «регулярные множества».
Кен Томпсон встроил их в редактор QED, а затем в редактор ed под UNIX. С этого времени регулярные выражения стали широко использоваться в UNIX и UNIX-подобных утилитах, например в expr, awk, Emacs, vi, lex и Perl.
Регулярные выражения в Perl и Tcl происходят от реализации, написанной Генри Спенсером. Филип Хейзел разработал библиотеку PCRE (англ. Perl-compatible regular expressions — Perl-совместимые регулярные выражения), которая используется во многих современных инструментах, таких как PHP и Apache.
Эти области изучают вычислительные модели (автоматы) и способы описания и
классификации формальных языков. В 1940-х гг. Уоррен Маккалок и Уолтер Питтс описали нейронную систему, используя простой автомат в качестве модели нейрона.
Математик Стивен Клини позже описал эти модели, используя свою систему математических обозначений, названную «регулярные множества».
Кен Томпсон встроил их в редактор QED, а затем в редактор ed под UNIX. С этого времени регулярные выражения стали широко использоваться в UNIX и UNIX-подобных утилитах, например в expr, awk, Emacs, vi, lex и Perl.
Регулярные выражения в Perl и Tcl происходят от реализации, написанной Генри Спенсером. Филип Хейзел разработал библиотеку PCRE (англ. Perl-compatible regular expressions — Perl-совместимые регулярные выражения), которая используется во многих современных инструментах, таких как PHP и Apache.
2019 March 22



Регулярные выражения в Python от простого к сложному

2019 March 23

Теория графов представляет собой один из наиболее важных и интересных, но в то же время один из самых сложных и непонятных разделов в информатике.
Понимание и использование графов делает нас более квалифицированными специалистами. По крайней мере, так должно быть. Граф – это множество вершин V и множество рёбер E, содержащих упорядоченную пару G=(V, E).
Пытаясь изучать теорию графов и реализовать некоторые алгоритмы, многие программисты просто прекращают этим заниматься, потому что считают данное занятие слишком скучным.
Лучший способ освоить что-то – понять, как и где оно применяется. В этой статье мы покажем различные примеры применения теории графов, проиллюстрировав каждый из них.
Пусть эта статья покажется слишком детальной для опытных программистов, но, поверьте, подробные объяснения гораздо эффективнее сжатых определений.
Понимание и использование графов делает нас более квалифицированными специалистами. По крайней мере, так должно быть. Граф – это множество вершин V и множество рёбер E, содержащих упорядоченную пару G=(V, E).
Пытаясь изучать теорию графов и реализовать некоторые алгоритмы, многие программисты просто прекращают этим заниматься, потому что считают данное занятие слишком скучным.
Лучший способ освоить что-то – понять, как и где оно применяется. В этой статье мы покажем различные примеры применения теории графов, проиллюстрировав каждый из них.
Пусть эта статья покажется слишком детальной для опытных программистов, но, поверьте, подробные объяснения гораздо эффективнее сжатых определений.
2019 March 24

Семь мостов Кёнигсберга
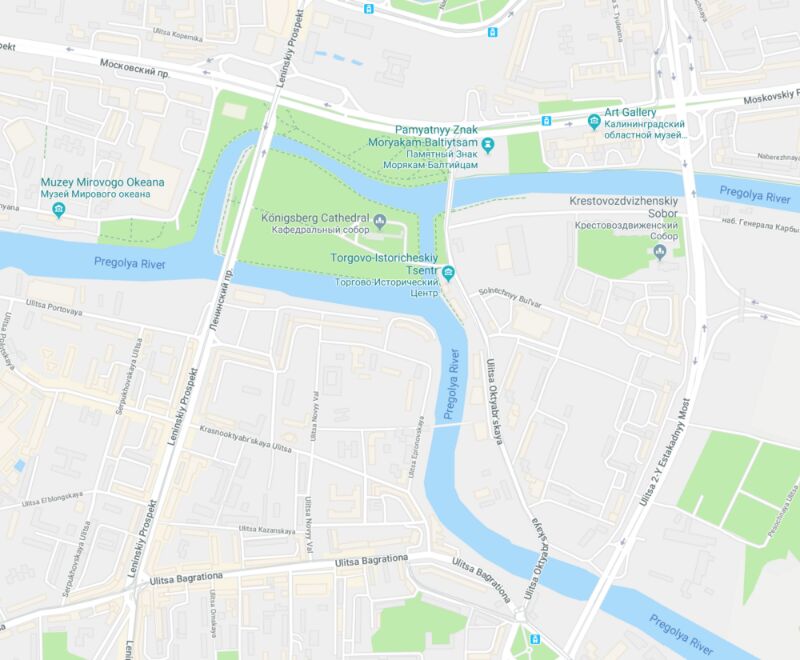
Начнём с того, с чем чаще всего сталкивается программист, читающий книгу про теорию графов – история про мосты и островы Калининграда. В Калининграде было семь мостов, соединяющих два больших острова, окруженных рекой Преголя, и две части материка, разделенные той же рекой.
Начнём с того, с чем чаще всего сталкивается программист, читающий книгу про теорию графов – история про мосты и островы Калининграда. В Калининграде было семь мостов, соединяющих два больших острова, окруженных рекой Преголя, и две части материка, разделенные той же рекой.

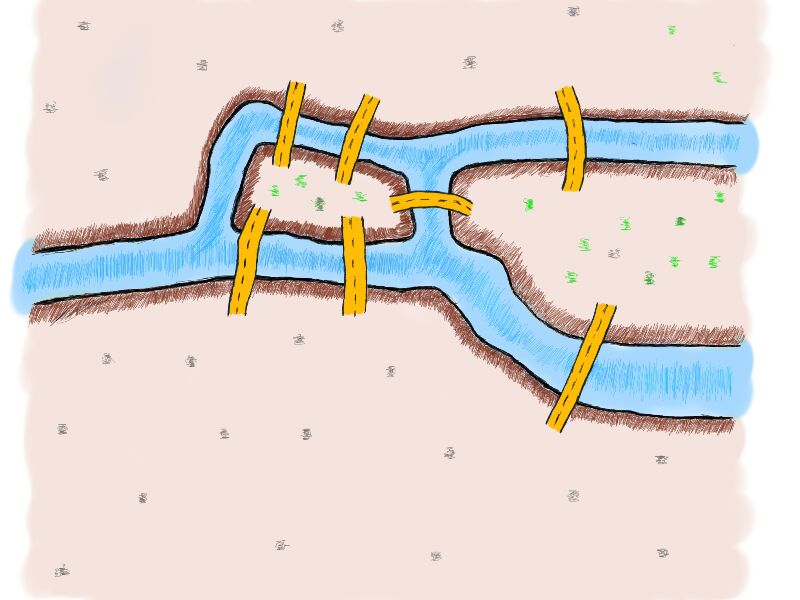
В 18 веке это был Кёнигсберг, город Пруссии, и на этой территории было гораздо больше мостов. Задача или просто головоломка состояла в том, что необходимо было найти такой маршрут, который проходил через каждый мост ровно один раз. Вот иллюстрированный вид семи мостов Кёнигсберга в 18 веке:

Попробуйте решить эту головоломку. Посмотрите, сможете ли вы пройти по всем мостам ровно один раз.
Непосещённых мостов быть не должно.
Пройти по мосту можно только один раз.
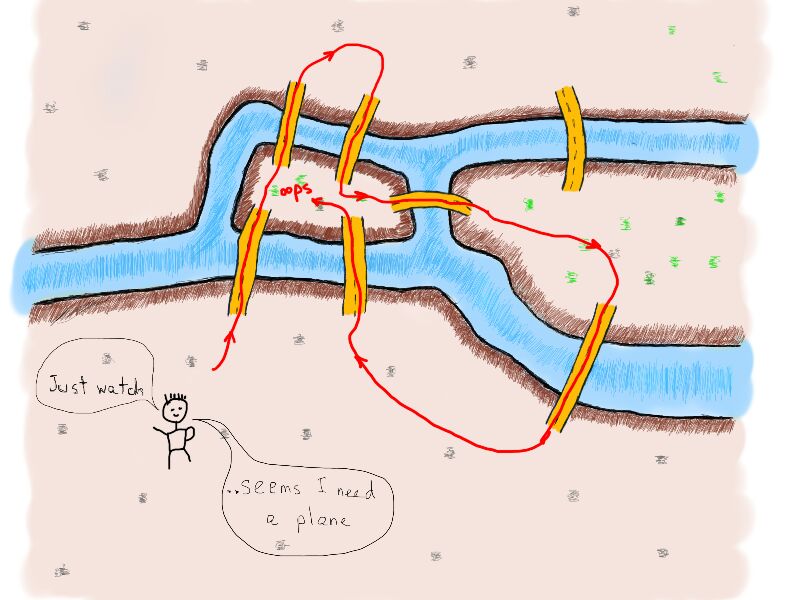
Если вы знакомы с этой задачей, то знаете, что это невозможно. Даже если вы очень сильно пытались, в конечном итоге вам пришлось сдаться.
Непосещённых мостов быть не должно.
Пройти по мосту можно только один раз.
Если вы знакомы с этой задачей, то знаете, что это невозможно. Даже если вы очень сильно пытались, в конечном итоге вам пришлось сдаться.

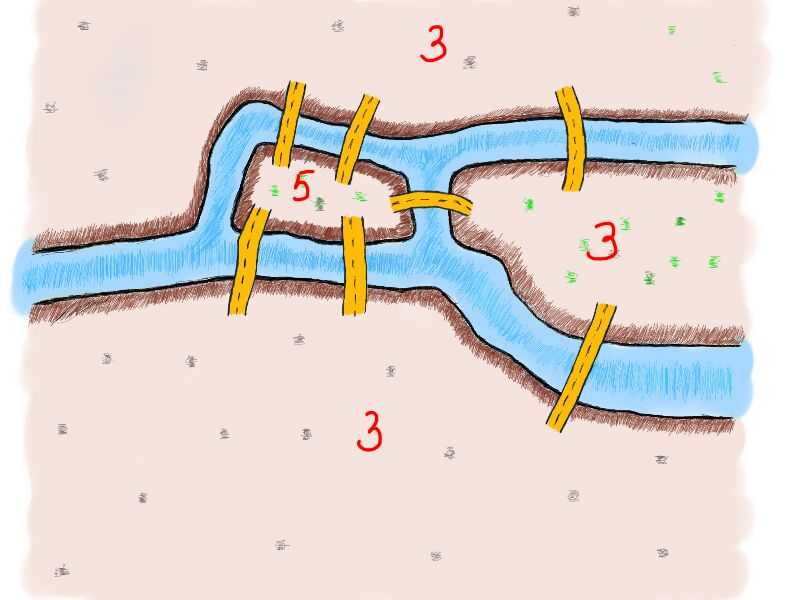
Есть четыре разных места: два острова и две части материка. И семь мостов. Интересно узнать, существует ли какая-либо закономерность в отношении количества мостов, связанных с островами или материком (мы будем использовать термин “земля” для обозначения четырех различных мест)?

На первый взгляд кажется, что это похоже на какой-то шаблон. Есть нечётное количество мостов, связанных с каждой землёй. Если нужно пересечь каждый мост один раз, то вам достаточно зайти на землю и сойти с неё, если она имеет два моста.
На рисунке выше видно, что если вы заходите на землю, проходясь по одному мосту, вы всегда можете покинуть землю, пройдя по её второму мосту. Всякий раз, когда появляется третий мост, вы не сможете покинуть землю, как только войдёте в нее.
Если вы попытаетесь обобщить это рассуждение для одного участка земли, то увидите, что в случае чётного количества мостов всегда можно покинуть землю, а в случае нечётного – нет.
На рисунке выше видно, что если вы заходите на землю, проходясь по одному мосту, вы всегда можете покинуть землю, пройдя по её второму мосту. Всякий раз, когда появляется третий мост, вы не сможете покинуть землю, как только войдёте в нее.
Если вы попытаетесь обобщить это рассуждение для одного участка земли, то увидите, что в случае чётного количества мостов всегда можно покинуть землю, а в случае нечётного – нет.

Изменим условие
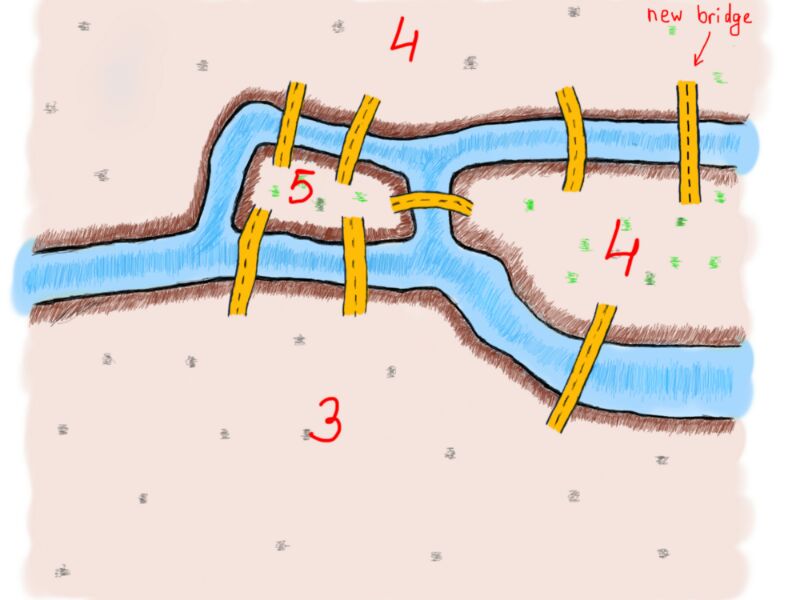
Давайте добавим новый мост, чтобы узнать, как изменится количество общих соединённых мостов, и решит ли он проблему:
Давайте добавим новый мост, чтобы узнать, как изменится количество общих соединённых мостов, и решит ли он проблему: