конечно) ты походу не понимаешь что аткое импорт)

я с веба пререшел на swift

gthtitk

перешел

в лс напиши, я раскажу)

если хочешь

всем привет, не могу url в instagram, то есть мне попасть в профиль? может кто знает?

и  facebook тоже

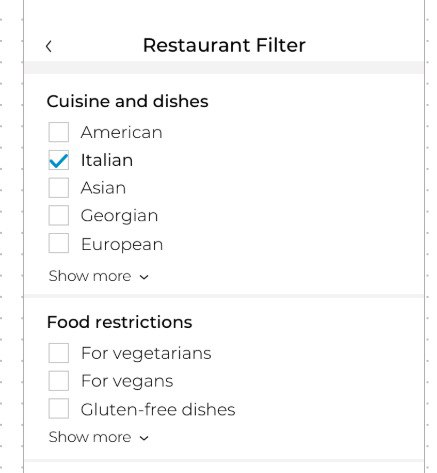
Правильно ли я понял, что это 2 секции tableview? И могу ли я сделать для них show more (сворачивание и разворачивание)?

ваши варианты реализации

1) количество чекбоксов - динамическая величина
2) анимация скрытия-раскрытия

Если честно, то это больше похоже на React/Cordova и прочее

чем?

Правильно это как?

Отсутствие гайдлайнов, шрифтов, чекбоксов и прочего. Такое ощущение, что это сверстали на css(less/sass)+html. Либо это вообще просто дизайн, который надо воплотить

Мего дизайнер

Всем привет. Взял на задание на codewars но не могу вкрутиь смылс, что делать надо)) Помоглите пжл

Common denominators

You will have a list of rationals in the form

{ {numer_1, denom_1} , ... {numer_n, denom_n} }
or

[ [numer_1, denom_1] , ... [numer_n, denom_n] ]
or

[ (numer_1, denom_1) , ... (numer_n, denom_n) ]
where all numbers are positive ints.

You have to produce a result in the form

(N_1, D) ... (N_n, D)
or

[ [N_1, D] ... [N_n, D] ]
or

[ (N_1', D) , ... (N_n, D) ]
or

{{N_1, D} ... {N_n, D}}
or

"(N_1, D) ... (N_n, D)"
depending on the language (See Example tests)

in which D is as small as possible and

N_1/D == numer_1/denom_1 ... N_n/D == numer_n,/denom_n.
Example:

convertFracs [(1, 2), (1, 3), (1, 4)] shouldBe [(6, 12), (4, 12), (3, 12)]
Note:
Due to the fact that first translations were written long ago - more than 4 years - these translations have only irreducible fractions. Newer translations have some reducible fractions. To be on the safe side it is better to do a bit more work by simplifying fractions even if they don't have to be.

Note for Bash:
input is a string, e.g "2,4,2,6,2,8"

output is then "6 12 4 12 3 12"