AG
Size: a a a
2020 March 04
Шурд, да
AG
он в принципе почти все и написал там
AG
по статье Йелле и Жюлса
ЗП
жаль это все приватное) я про код
AG
ну в перспективе код откроем
AG
но пока так
ЗП
я знаю у вас еще и пурса?
AG
ага
O
региться куда-то чтоб поюзать композиции функций, хм
ЗП
по статье Йелле и Жюлса
это что-то про струнные диаграммы?
AG
это что-то про струнные диаграммы?
Oℕ
ну напиши)
что написать?
Oℕ
ну напиши)
Если ты про свой грязный хошкел опять, то ну грубо говоря бифунктор можно расширить вдоль другого бифунктора.
Соответственно, у тебя два варианта - тот другой - это бифунктор (Set, Set) -> Set тогда расширение будет очевидно эндофунктором в Set:
Если ты хочешь, чтобы расширение было бифунктором, то расширять нужно вдоль какого-то двухзначного функтора.
Ну в плохих языках, его обжект мэппинг мог бы иметь такой тип
Тогда расширения выглядели бы так
type Ran t k c d = forall a b. ( c -> k a b False) -> (d -> k a b True) -> t a b
type Lan t k c d = exists a b.(k a b False -> c, k a b True -> d, t a b)
Соответственно, у тебя два варианта - тот другой - это бифунктор (Set, Set) -> Set тогда расширение будет очевидно эндофунктором в Set:
type Ran t k c = forall a b. ( c -> k a b) -> t a b
type Lan t k c = exists a b.(k a b -> c, t a b)
Если ты хочешь, чтобы расширение было бифунктором, то расширять нужно вдоль какого-то двухзначного функтора.
Ну в плохих языках, его обжект мэппинг мог бы иметь такой тип
Type -> Type-> Bool -> Type
Тогда расширения выглядели бы так
type Ran t k c d = forall a b. ( c -> k a b False) -> (d -> k a b True) -> t a b
type Lan t k c d = exists a b.(k a b False -> c, k a b True -> d, t a b)
Oℕ
Эх, а со мной не поздоровались
ЗП
Если ты про свой грязный хошкел опять, то ну грубо говоря бифунктор можно расширить вдоль другого бифунктора.
Соответственно, у тебя два варианта - тот другой - это бифунктор (Set, Set) -> Set тогда расширение будет очевидно эндофунктором в Set:
Если ты хочешь, чтобы расширение было бифунктором, то расширять нужно вдоль какого-то двухзначного функтора.
Ну в плохих языках, его обжект мэппинг мог бы иметь такой тип
Тогда расширения выглядели бы так
type Ran t k c d = forall a b. ( c -> k a b False) -> (d -> k a b True) -> t a b
type Lan t k c d = exists a b.(k a b False -> c, k a b True -> d, t a b)
Соответственно, у тебя два варианта - тот другой - это бифунктор (Set, Set) -> Set тогда расширение будет очевидно эндофунктором в Set:
type Ran t k c = forall a b. ( c -> k a b) -> t a b
type Lan t k c = exists a b.(k a b -> c, t a b)
Если ты хочешь, чтобы расширение было бифунктором, то расширять нужно вдоль какого-то двухзначного функтора.
Ну в плохих языках, его обжект мэппинг мог бы иметь такой тип
Type -> Type-> Bool -> Type
Тогда расширения выглядели бы так
type Ran t k c d = forall a b. ( c -> k a b False) -> (d -> k a b True) -> t a b
type Lan t k c d = exists a b.(k a b False -> c, k a b True -> d, t a b)
очень странно выглядит этот Bool
Oℕ
очень странно выглядит этот Bool
ну предложи другой способ определить конструктор пары типов (Type, Type) -> (Type, Type)
2020 March 06
ЮБ
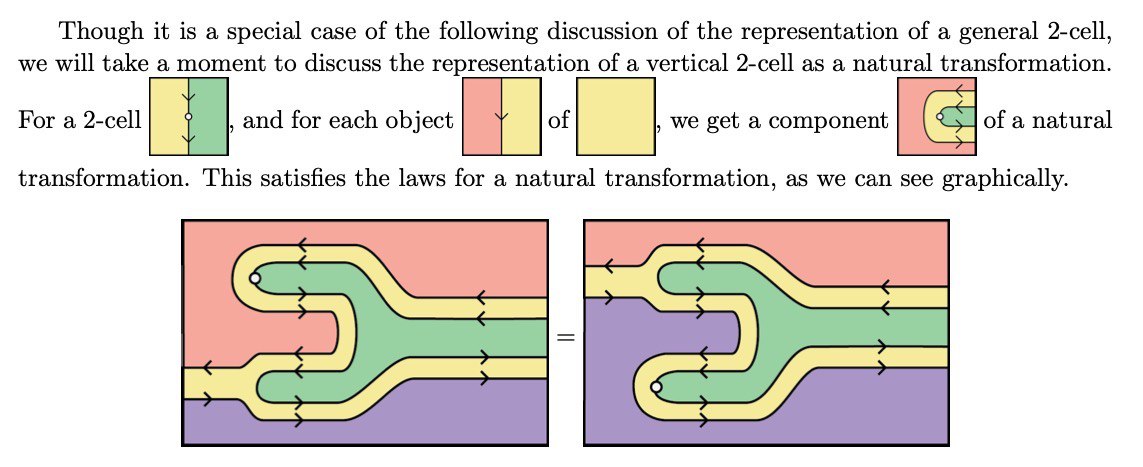
Я тут почти случайно открыл пейпер «A Yoneda-style embedding for virtual equipments» и увидел внутри вот это.
Кто-нибудь встречал подобную графическую нотацию ранее? Похоже на string diagrams, но не совсем.
Кто-нибудь встречал подобную графическую нотацию ранее? Похоже на string diagrams, но не совсем.
ЗП

Я тут почти случайно открыл пейпер «A Yoneda-style embedding for virtual equipments» и увидел внутри вот это.
Кто-нибудь встречал подобную графическую нотацию ранее? Похоже на string diagrams, но не совсем.
Кто-нибудь встречал подобную графическую нотацию ранее? Похоже на string diagrams, но не совсем.
это и есть струнные диаграммы
ЮБ
это и есть струнные диаграммы
Окей, спасибо. Честно говоря, впервые увидел, чтобы их раскрашивали.
Oℕ
Это просто 2-мерные



