Все ок, так то изначально верно сделал что ограничил.

Ну скажем ребер то может быть и больше, вопрос был в том если я нахожу безопасные ребра и уже нашел V-1 штук то дальше не надо искать. верно же

,

Просто в Кормен(книга) этой условии нету, и он даже на рисунке показывает как после нахождении V -1 он продолжает искать. Поэтому и подумал что что то не понимаю

Если ты добавил V-1 ребро, то ясно что больше ни одно ребро добавлено (без удаления имеющихся) быть не может. При этом ни одно из уже взятых ребер не может быть выкинуто. Значит остальные ребра можно проскипать.

СПС!!! Я просто из за книги Кормена запутался)

is the REST concept a good method of server-client implementation and synchronization

for example, equivilant to

cout << "invoking server side function" << endl;
auto returnCode = server.InvokeBlockingFunction("FUNCTION");
cout << "server side function returned " << returnCode << endl;

Может кто пояснить насчёт минимального и наименьшего элементов множества? Правильно ли я понимаю, что множество, включающее множество букв кириллического алфавита и множество цифр будет иметь, 2 минимальных элемента: "я" и "0", при том не будет иметь наименьшего?

Насколько я помню из курса универской алгебры, эти понятия связаны с понятием порядка/частичного порядка на множестве, т.е. мы привыкли, что ...-1 < 0 < 1 < 2..., но кто запрещает ввести какой-то свой порядок на данном множестве, например, положить, что любой отрицательный элемент больше любого положительного, а между собой они сравниваются по модулю, тогда 0 < 1 < 2 < ... < -1 < -2 и т.п., можно ввести такой порядок, что множество разобьётся на несколько подмножеств, таким образом, что два элемента из разных подмножеств просто нельзя будет сравнить. Соответственно, в вашем примере всё зависит от того, какие правила сравнения вы введёте для множества цифр + алфавита, например если условиться, что между собой цифры и буквы несравнимы, но внутри подможеств возможно сравнение в лексикографическом порядке, то вы получите множество разбитое на две цепи (цифры с минимальным элементом 0 и символы с минимальным элементом а), но установить наименьший элемент не получится, т.к. неизвестен способ сравнения а и 0. А вот если приписать всем элементам специальные коды, или условится, что, например, любая цифра заранее меньше символа, то наименьший элемент появится - 0.
З.Ы. Позволил себе не проверять упомянутые способы сравнения на соответствие свойствам, которые должны быть у отношения частичного порядка, коротко прочитать про всё это можно тут https://ru.wikipedia.org/wiki/%D0%A7%D0%B0%D1%81%D1%82%D0%B8%D1%87%D0%BD%D0%BE_%D1%83%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BE%D1%87%D0%B5%D0%BD%D0%BD%D0%BE%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE

雾霾

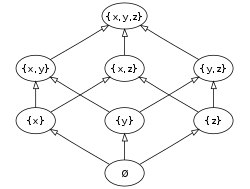
,это вроде куб?

Это схема частично упорядоченного множества из 3 элементов, ничего не мешает часть стрелок вытянуть или изогнуть - смысл от этого ничуть не поменяется

А гипергуб получится?

Ну, определенная связь между множеством всех подмножеств K-элементного множества и K-гиперкубом есть.

При этом отношение частичного порядка становится таким: "для каждого i A_i <= B_i".

Разве на нее можно ЦД упихать?

Вроде там за линию есть

У кого-то упихать удалось

Нифига

Там, например, надо перенумеровать вершины в порядке tin