сразу видно что у чела математический склад ума)

ну кароч богатым будет через 10 лет, да?

сейчас скажу

по идее вот так

о, щас прочитаю

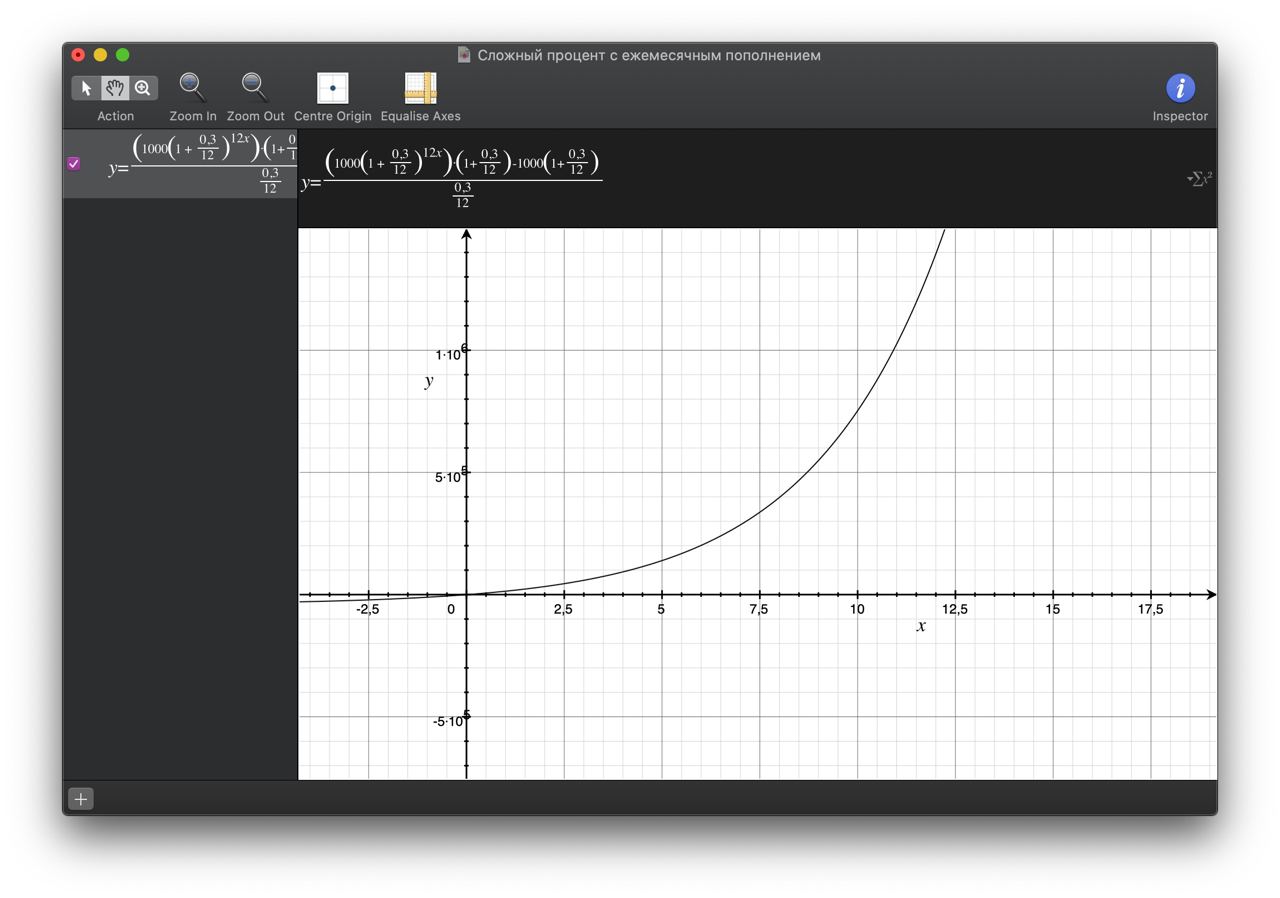
1. Сумма первоначальных инвестиций наращивается по указанной процентой ставке в соответствии с заданным сроком

Sинв - сумма первоначальных инвестиций (в Вашем случае 1млн)
Sпополн - сумма, на которую осуществляется периодическое пополнение (в Вашем случае 1млн)
Кпер - количество периодов (в Вашем случае 3)
%ставка - ставка в процентах за один период (в Вашем случае 30%)

Сумма, которую дадут первоначальные инвестиции:
FV1=Sинв*(1+%ставка/100)^Кпер

2. Суммы ежегодного пополнения тоже наращиваются, при этом поскольку каждое последующее пополнение "работает", т.е. приносит проценты, на 1 год меньше предыдущего, то в результате наращивания эти суммы ежегодного пополнения образуют элементы геометрической прогрессии со знаменателем (1+%ставка/100), и их удобно учитывать по формуле суммы членов геометрической прогрессии.

Первый член геометрической прогрессии (наращенная сумма пополнения в начале заключительного периода)
b1=Sпополн^(1+%ставка/100)
Знаменатель прогрессии
q=(1+%ставка/100)
Число членов геометрической прогрессии, для которых рассчитывается сумма (число пополнений)
n=Кпер-1
Сумма n первых членов геометрической прогрессии (она же сумма, которую даст периодическое пополнение)
FV2= b1*(1-q^n)/(1-q)=Sпополн^(1+%ставка/100)*(1-(1+%ставка/100)^(Кпер-1))/(1-(1+%ставка/100))

3. Сумма, которая получается в результате
FV=FV1+FV2

если что я не сам это написал, но согласен с логикой, которая тут написана, потому что меня смутила арифметическая прогрессия и я полез убедиться, что смутился не зря

ну вот я по геометрической считал

ты калькулятор делаешь что ли?

или пытаешься понять сколько нужно докидывать чтобы стать миллионером?)

да, так выглядит логичнее)

+

изучаю математику и ее применение в жизни

да, как говорил мой один друг - ничто так не вселяет надежду на светлое будущее, как сложные проценты

скриншот низзя было приаттачить? зачем пдвку кинул? )))

это grapher так экспортит на ctrl + c

А сколько нужно? что говорят рассчеты? я тоже хочу миллионером 🙂