/text

​📋 Пост в группе Мехмат МГУ:

Мастерская Петра Фоменко приглашает на СЕГОДНЯ, желающие получить бесплатные пригласительные пишите напрямую Кате, обязательно указать фамилию, имя, количество билетов и номер курса.

9 марта (вт) 19:00 "Король Лир" постановка  Евгений Каменькович, в ролях - Карен Бадалов, Юрий Буторин, Полина Кутепова.
«На сцене - ничего лишнего, каждая деталь имеет свое значение и используется настолько тонко и многогранно, что диву даёшься! Сцена, которая одновременно и королевство, и комната, и тюремные колодки, и куст, и кровать. Красные перчатки, которые дочери Лира надевают в конце, как кровь на их руках. Черный язык клеветника, трость-меч, чан с водой как зеркало. Перечислять можно долго, в ткани спектакля эти акценты как жемчужинки..Самое яркое впечатление для меня - сцены битвы и бури. Очень красиво и оригинально.»

Описание и отзывы можно прочитать по ссылке: https://biletyotkati.ru/event/11208

Желаю в каждый дом такого гостя

​А какой у вас любимый способ построения курса матана?

📢 Репост из группы Ёжик в матане:

Дорогие коллеги!

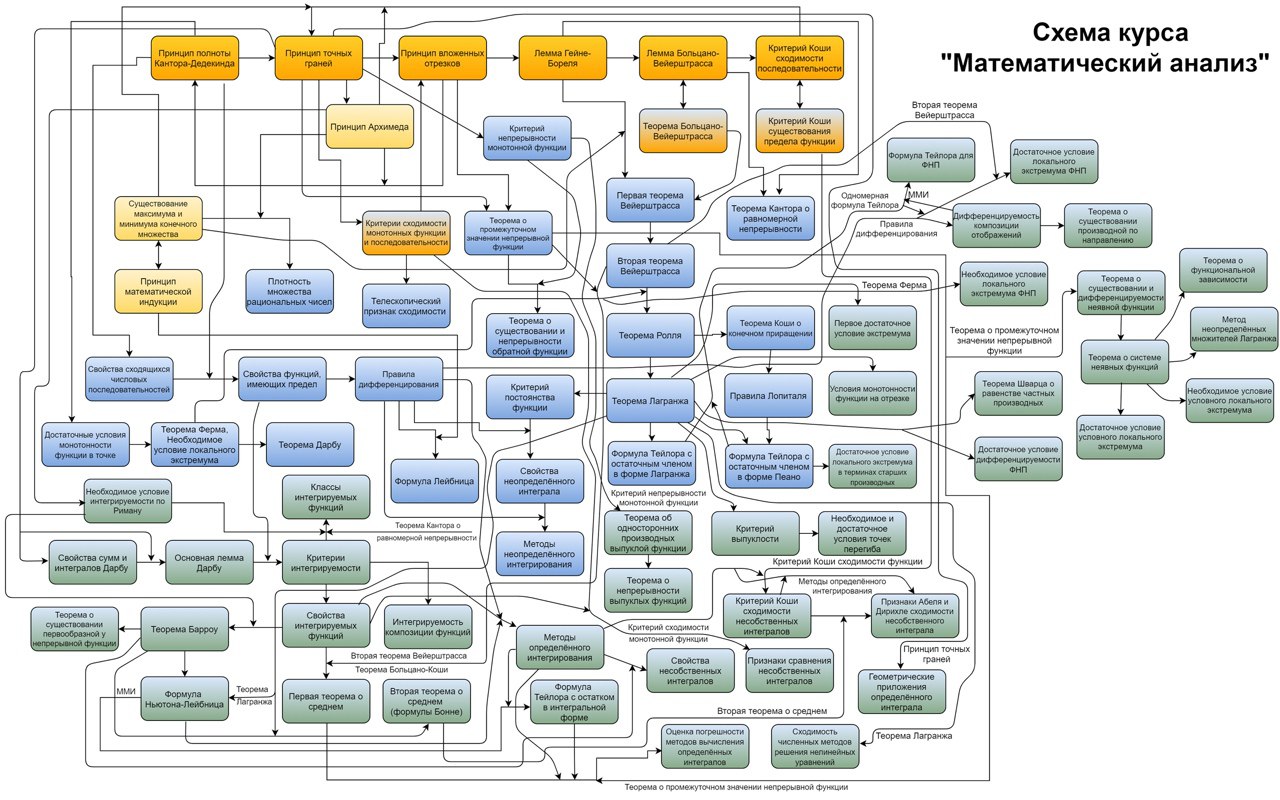
В этот вторник, в замечательной группе Математика – Просто | Алексей Савватеев была опубликована схема курса математический анализ, к созданию которой я когда-то приложил руку 😊

https://vk.com/alexei_savvateev?w=wall-148115211_32408

Оказалось, что данная тема достаточно интересна широкой публике. Поэтому, я решил выложить в субботу данную схему и у нас, снабдив её своими комментариями.

Можно легко заметить, что входа на этой схеме нет. В качестве оного может быть выбран любой принцип полноты (или любая теорема полноты), которые отмечены оранжевым цветом. Все они эквивалентные. Т.е. мы можем любой из них принять за изначальную аксиому, и вывести из неё весь курс математического анализа. Тут важно, правда, отметить, что к четырём последним обязательно требуется добавить аксиому Архимеда. Т.е. они являются равнозначными остальным лишь в архимедовых полях.

Жёлтым цветом отмечены вспомогательные утверждения, с помощью которых курс строится проще.

Оранжево-синим цветом отмечены теоремы, эквивалентные всем принципам полноты, но их обычно за изначальные принципы полноты не принимают, а считают именно теоремами.

Разделение на синий и зелёный цвета несколько условное. Я делал это для "визуального эффекта", и отметил синим то, что на нашем факультете (ВМК МГУ) проходится в первом семестре, зелёным, то что во втором

В нашей группе я дополнительно выкладываю отличную статью J.F. Hall "Completeness of Ordered Fields", в которой вопрос об эквивалентности принципов полноты рассматривается существенно глубже, чем в моём курсе, и откуда я, в своё время, взял несколько интересных идей!

P.S. Большое спасибо Егору Кузьмичёву за обозначенную выше оригинальную публикацию!

— Приложение:
Hall - Completeness of Ordered Fields.pdf, 281 Кб

​Пау-пау

📢 Репост из группы Спорт на мехмате:

Обзор секции: дуэльная стрельба

#снмм_обзор_секции

Следующей секцией, о которой мы бы хотели рассказать, является дуэльная стрельба!

Дуэльная стрельба — командное упражнение по стрельбе из винтовок/пистолетов.

Две команды стрелков, по сигналу судьи, из старта лёжа бегом должны достигнуть огневого рубежа, зарядить оружие и из положения лёжа/стоя поразить установленные на специальной линии две группы мишеней, по группе для каждой команды. Каждая мишень в группе условно обозначает конкретного стрелка команды противника и если она поражена, то стрелок команды противника, которого условно обозначала мишень, считается выбывшим и лишается права продолжать стрельбу.

Победа присуждается команде стрелков, раньше противника поразившей свою группу мишеней.

Что сказать, дуэльная стрельба — это зрелищно! В этом матче участвуют лучшие стрелки основного матча и зачастую лучшие стрелки страны. В дуэльной стрельбе можно увидеть битвы характеров, техник и гейм-планов.

— Ссылка:
Обзор секций

​📢 Репост из группы Кафедра дифференциальной геометрии и приложений:

Выкладываем видео, слайды и материалы к 4-й лекции Лектория для 1-2 курса "Современная геометрия", лекторы: профессора А.Б.Жеглов и В.В.Пржиялковский 27 февраля 2021 года.

Тема лекции: «Алгебраическая геометрия и ее приложения»
Анонс этой лекции: пост https://vk.com/wall-193252362_83

Вопросы по лекции и по нашей теме можно писать по почте лекторам (можно также дублировать их также в ЛС нашей группы) :
Александр Борисович Жеглов azheglov@mech.math.msu.su
Виктор Владимирович Пржиялковский victorprz@mi-ras.ru

С удовольствием ответим на возникшие у Вас вопросы :)
Приятного просмотра!

Краткий список тем:
— история алгебраической геометрии, заметные открытия и специалисты
— диофантовы уравения, пифагоровы тройки, эллиптические кривые и теорема Ферма
— системы полиномиальных уравнений, кольца дифференциальных операторов,
— зеркальная симметрия, связи с теорией струн, модели Ландау-Гинзбурга.

Учебный курс + семинар
В следующем учебном году 21/22 проф. В.В.Пржиялковский будет читать курс по алгебраической геометрии на 3м курсе программы "Фундаментальная математика и математическая физика" на мехмате (спецпоток, подробнее о нем https://fmmp.math.msu.ru/ )

Информация о лекторах:
http://dfgm.math.msu.su/people/zheglov/
http://dfgm.math.msu.su/people/przyjalkowski/ а также http://www.mi-ras.ru/~victorprz/index.htm

Видеозапись доступна для просмотра и скачивания также на сайте кафедры:
http://dfgm.math.msu.su/files/lectorium/ZheglovPrzyjalkowski.mp4
и на гугл-диске Лектория:
https://goo.su/4EsV (вводите в адресную строку)

Литература:
есть две книги по алгебраической геометрии (вводные, но не очень простые). Майлз Рид и Хатчер. По своей теме А.Б.Жеглова есть подготовленный им учебник по итогам преподавания в Шеньчжене, КНР, в 19 году. Они непростые, но интересующиеся могут посмотреть.

— Видео:
Алгебраическая геометрия и ее приложения. Лекция 4. А.Б.Жеглов, В.В.Пржиялковский 27.02.21, 1:34:45

— Приложения:
Слайды Лекции 4 Жеглов Пржиялковский 27_02_21.pdf, 856 Кб
Жеглов Lectures_DO_semester_1.pdf, 1.1 Мб
Хатчер алгебраическая геометрия начальный курс.pdf, 44.3 Мб
Майлз Рид алгебраическая геометрия для всех.djvu, 1.6 Мб

— Ссылка:
Архив Лектория для 1-2 курса "Современная геометрия"

​📢 Репост из группы ЛЮДИ МЕХМАТА:

В этот прекрасный весенний день приглашаем вас к просмотру интервью со Шкляевым Александром Викторовичем.

Сегодня вы узнаете...
▪как преподаватели относятся к работе во время учебы
▪где работают студенты после обучения на кафедре "Математической статистики"
▪почему мехмат учит чтению и откуда взялось слово "тривиально"

Ребята, спасибо за комментарии к прошлому видео. Вы помогаете становиться нам лучше!

Наверняка заметно, что мы немного изменили формат. Будем рады услышать ваше впечатления по ссылке:  https://docs.google.com/forms/d/e/1FAIpQ...6HjeQ2GpFTV3Bmebg/viewform?usp=pp_url

Приятного просмотра!

— Видео:
Люди мехмата: Александр Викторович Шкляев, 1:08:12

— Ссылка:
Обратная связь

​Всем бы кафедрам таких сммщиков!

📢 Репост из группы Кафедра математической логики МГУ:

#матлог

Непонятно, что происходит на этом фото?

Это Мати Рейнович Пентус (зам.зав.кафедрой!) рассказывает про свою область интересов - исчисление Ламбека 😱

Чтобы побольше узнать про эту и другие возможности исследований на кафедре математической логики и теории алгоритмов, приходи 19 марта в 16:45 на встречу с кафедрой, выбирай научного руководителя и постигай науку!

а причем тут SMM? Типа, псс парень, хочешь вкурить что показано на слайде, тогда иди к нам, мы тебе отсыпем.

Чето я выпал

Решил использовать файловую систему с тегами, а не с директориями

Потому что дерево директорий неудобное

Я хз как задавать удобную иерархию файлов

Ебал иерархию

Хуйня выходит в итоге

#py print("ksat/")

python3 | 3.7.4

ksat/

CPU Time: 0.02 s
Memory: 7728 KB