RB
Size: a a a
2021 February 24
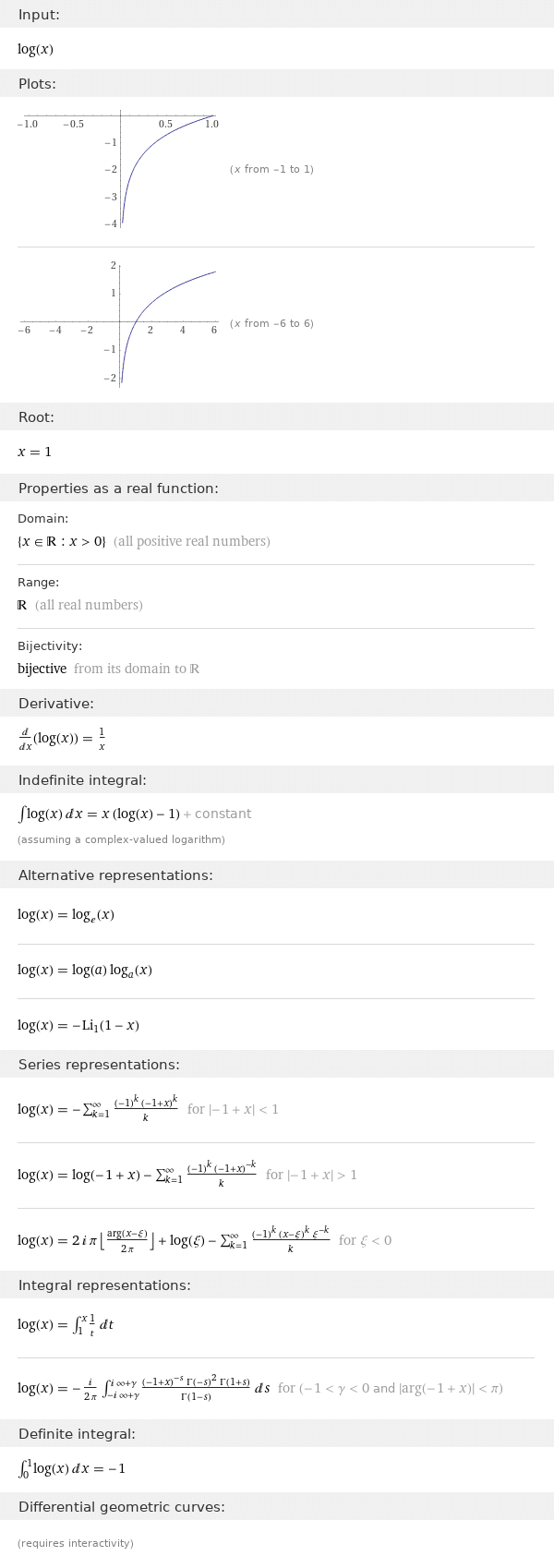
/wf ln(x)
M
/wf ln(x)
NK
Это наше национальное достояние
📢 Репост из группы Спорт на мехмате:
Обзор секции: гандбол
#cнмм_обзор_секции
Наш первый обзор ЦС мы бы хотели посвятить гандболу! Мы взяли интервью у одного из студентов, который занимается гандболом в секции. Его рассказ можно прочитать в статье ниже.
Но для начала давайте разберемся, что это за игра и какие у нее правила.
Первые упоминания об игре с мячиком, напоминающей гандбол, были найдены исследователями в известнейшем произведении Гомера — «Одиссея». Затем о ней писал древнеримский врач Галенус.
Гандбол – командная игровой вид спорта, целью в котором является забросить как можно больше мячей в ворота соперника. В отличие от футбола, мяч забрасывают руками.
В состав команды входит 16 игроков, из которых на поле одновременно могут появиться 7 — шесть полевых и один вратарь. Матчи состоят из двух таймов по 30 минут с перерывом в 15 минут.
В начале матча игроки должны ввести мяч в игру с центра поля. Спортсмены могут касаться предмета игры любыми частями тел, исключая ноги. Перед тем как сделать пас товарищу по команде либо выполнить бросок по воротам соперника, игрок имеет право удерживать мяч не более 3 секунд.
Владея мячом, спортсмен может сделать максимум три шага. После этого предстоит ударить предмет игры о площадку, отдать передачу партнеру либо выполнить бросок по воротам. Тренер каждой команды во время матча имеет право взять по одному тайм-ауту, длительностью в 1 минуту.
— Ссылка:
Обзор секций
📢 Репост из группы Спорт на мехмате:
Обзор секции: гандбол
#cнмм_обзор_секции
Наш первый обзор ЦС мы бы хотели посвятить гандболу! Мы взяли интервью у одного из студентов, который занимается гандболом в секции. Его рассказ можно прочитать в статье ниже.
Но для начала давайте разберемся, что это за игра и какие у нее правила.
Первые упоминания об игре с мячиком, напоминающей гандбол, были найдены исследователями в известнейшем произведении Гомера — «Одиссея». Затем о ней писал древнеримский врач Галенус.
Гандбол – командная игровой вид спорта, целью в котором является забросить как можно больше мячей в ворота соперника. В отличие от футбола, мяч забрасывают руками.
В состав команды входит 16 игроков, из которых на поле одновременно могут появиться 7 — шесть полевых и один вратарь. Матчи состоят из двух таймов по 30 минут с перерывом в 15 минут.
В начале матча игроки должны ввести мяч в игру с центра поля. Спортсмены могут касаться предмета игры любыми частями тел, исключая ноги. Перед тем как сделать пас товарищу по команде либо выполнить бросок по воротам соперника, игрок имеет право удерживать мяч не более 3 секунд.
Владея мячом, спортсмен может сделать максимум три шага. После этого предстоит ударить предмет игры о площадку, отдать передачу партнеру либо выполнить бросок по воротам. Тренер каждой команды во время матча имеет право взять по одному тайм-ауту, длительностью в 1 минуту.
— Ссылка:
Обзор секций
VB
Ребят, есть что-то по дробному дифферинтегрированию ?
AK
Тока по картечному интегрифинцированию...
NK
📢 Репост из группы Кафедра математической логики МГУ:
#матлог #учёба #спецсеминар
На онлайн-заседании объединенного семинара кафедры математической логики и теории алгоритмов МГУ
"Модальная и алгебраическая логика" и "Логические методы в информатике"
в ближайший четверг 25 февраля, начало в 18:30, состоится продолжение доклада
Т. Г. Пшеницын
Гиперграфовые грамматики Ламбека
Данный доклад (который, вероятно, займет 2 лекции) продолжает тематику докладов по обобщению исчисления Ламбека на гиперграфы, однако посвящен принципиально новому разделу — грамматикам. Гиперграфовое исчисление Ламбека возникло из желания совместить принципы обычного исчисления Ламбека с принципами грамматик замещения гиперребер. В частности, по аналогии с обычными грамматиками Ламбека, можно определить гиперграфовые грамматики Ламбека (ГГЛ). Эти грамматики представляют собой альтернативный грамматикам замещения гиперребер формализм для порождения гиперграфовых языков. Будет показано, что ГГЛ, с незначительными исключениями, порождают все контекстно-свободные гиперграфовые языки (что является прямым обобщением теоремы Гайфмана). Также будет доказана NP-полнота проверки принадлежности гиперграфа языку, задаваемому данной ГГЛ.
Ключевой вопрос, на который будет дан ответ в данном докладе — выполняется ли для ГГЛ теорема Пентуса: верно ли, что всякий язык, порождаемый ГГЛ, является контекстно-свободным? Несколько неожиданный ответ — нет. Так, данные грамматики могут порождать язык всех графов без изолированных вершин, язык всех двудольных графов без изолированных вершин. Кульминационный результат заключается в том, что ГГЛ порождают конечные пересечения контекстно-свободных гиперграфовых языков. Из этого будет следовать в том числе, что ГГЛ могут порождать строковые языки, которые не порождаются грамматиками замещения гиперребер, а также то, что для них не выполняется теорема Парика.
Видеозаписи предыдущих докладов:
https://www.youtube.com/playlist?list=PLEBNQnjHceeVxr2o766qqr993dyaKWRCX
Веб-страница с аннотациями и слайдами:
http://lpcs.math.msu.su/rus/ml.htm
Для получения ссылки на конференцию Zoom пишите на почту aleksandr.zapryagaev@yandex.ru.
Убедительно просим всех подключающихся указывать в Zoom свои настоящие имя и фамилию!
#матлог #учёба #спецсеминар
На онлайн-заседании объединенного семинара кафедры математической логики и теории алгоритмов МГУ
"Модальная и алгебраическая логика" и "Логические методы в информатике"
в ближайший четверг 25 февраля, начало в 18:30, состоится продолжение доклада
Т. Г. Пшеницын
Гиперграфовые грамматики Ламбека
Данный доклад (который, вероятно, займет 2 лекции) продолжает тематику докладов по обобщению исчисления Ламбека на гиперграфы, однако посвящен принципиально новому разделу — грамматикам. Гиперграфовое исчисление Ламбека возникло из желания совместить принципы обычного исчисления Ламбека с принципами грамматик замещения гиперребер. В частности, по аналогии с обычными грамматиками Ламбека, можно определить гиперграфовые грамматики Ламбека (ГГЛ). Эти грамматики представляют собой альтернативный грамматикам замещения гиперребер формализм для порождения гиперграфовых языков. Будет показано, что ГГЛ, с незначительными исключениями, порождают все контекстно-свободные гиперграфовые языки (что является прямым обобщением теоремы Гайфмана). Также будет доказана NP-полнота проверки принадлежности гиперграфа языку, задаваемому данной ГГЛ.
Ключевой вопрос, на который будет дан ответ в данном докладе — выполняется ли для ГГЛ теорема Пентуса: верно ли, что всякий язык, порождаемый ГГЛ, является контекстно-свободным? Несколько неожиданный ответ — нет. Так, данные грамматики могут порождать язык всех графов без изолированных вершин, язык всех двудольных графов без изолированных вершин. Кульминационный результат заключается в том, что ГГЛ порождают конечные пересечения контекстно-свободных гиперграфовых языков. Из этого будет следовать в том числе, что ГГЛ могут порождать строковые языки, которые не порождаются грамматиками замещения гиперребер, а также то, что для них не выполняется теорема Парика.
Видеозаписи предыдущих докладов:
https://www.youtube.com/playlist?list=PLEBNQnjHceeVxr2o766qqr993dyaKWRCX
Веб-страница с аннотациями и слайдами:
http://lpcs.math.msu.su/rus/ml.htm
Для получения ссылки на конференцию Zoom пишите на почту aleksandr.zapryagaev@yandex.ru.
Убедительно просим всех подключающихся указывать в Zoom свои настоящие имя и фамилию!
NK
📋 Пост в группе Мехмат МГУ:
Кафедра математических и компьютерных методов анализа начинает читать новый спецкурс «Информационная безопасность для разработчиков» совместно с компанией «ПАРАЛЛЕЛС (COREL RUSSIA)»
Ссылку на конференцию в Teams вы можете найти по адресу: https://mkma.math.msu.su/uchebnaya-deyatelnost/raspisanie_spetskursov/
На курсе вы узнаете:
- общие понятия безопасности (дефект, уязвимость, свойства информации, угрозы, и т.п.).
- применение безопасности на разных этапах жизненного цикла продукта (Microsoft SDL)
- основные ошибки и атаки
- принципы безопасного дизайна
- принципы безопасной имплементации
- моделирование угроз
- серверная и клиентская безопасность
- модель безопасности Web-браузера, безопасность Web-приложений
- аутентификация, авторизация, контроль доступа, сессии
- принципы применения криптографии
— Ссылка:
Расписание спецкурсов — Кафедра математических и компьютерных методов анализа
Кафедра математических и компьютерных методов анализа начинает читать новый спецкурс «Информационная безопасность для разработчиков» совместно с компанией «ПАРАЛЛЕЛС (COREL RUSSIA)»
Ссылку на конференцию в Teams вы можете найти по адресу: https://mkma.math.msu.su/uchebnaya-deyatelnost/raspisanie_spetskursov/
На курсе вы узнаете:
- общие понятия безопасности (дефект, уязвимость, свойства информации, угрозы, и т.п.).
- применение безопасности на разных этапах жизненного цикла продукта (Microsoft SDL)
- основные ошибки и атаки
- принципы безопасного дизайна
- принципы безопасной имплементации
- моделирование угроз
- серверная и клиентская безопасность
- модель безопасности Web-браузера, безопасность Web-приложений
- аутентификация, авторизация, контроль доступа, сессии
- принципы применения криптографии
— Ссылка:
Расписание спецкурсов — Кафедра математических и компьютерных методов анализа
NK
📢 Репост из группы Математура: книги издательства МЦНМО:
В последнее время в медиа все чаще пишут, что если показать ученикам связь математики с практическими ситуациями, это повысит мотивацию к учёбе.
Мы выпустили отдельной брошюрой статьи А.Н.Колмогорова "Математика", написанные им для разных изданий БСЭ. В частности, А.Н. пишет и о математике в школе. Вот что он говорит о стремлении связать изучение математики с практическими задачами (большая цитата, чтобы сохранить контекст):
Несмотря на все трудности первых лет существования молодой Советской республики, проводилась интенсивная и плодотворная работа по созданию нового школьного курса математики, соответствующего общим принципам советской педагогики. Были разработаны программы по математике применительно к принципу трудовой школы, появился ряд новых учебников и учебных пособий, обеспечивавших возможность работы по этим программам. Однако при этом были допущены и серьезные ошибки, основанные на ложной теории отмирания школы и на стремлении связать с практическими задачами изучение каждого раздела школьной математики, даже если это нарушало стройность и систематичность изложения.
А как вы думаете, полезно ли в старших классах показывать связь математики с практикой? Повышает ли это мотивацию? Углубляет ли знания?
— Ссылка:
Единство математики | Колмогоров А. Н. | Издательство МЦНМО
В последнее время в медиа все чаще пишут, что если показать ученикам связь математики с практическими ситуациями, это повысит мотивацию к учёбе.
Мы выпустили отдельной брошюрой статьи А.Н.Колмогорова "Математика", написанные им для разных изданий БСЭ. В частности, А.Н. пишет и о математике в школе. Вот что он говорит о стремлении связать изучение математики с практическими задачами (большая цитата, чтобы сохранить контекст):
Несмотря на все трудности первых лет существования молодой Советской республики, проводилась интенсивная и плодотворная работа по созданию нового школьного курса математики, соответствующего общим принципам советской педагогики. Были разработаны программы по математике применительно к принципу трудовой школы, появился ряд новых учебников и учебных пособий, обеспечивавших возможность работы по этим программам. Однако при этом были допущены и серьезные ошибки, основанные на ложной теории отмирания школы и на стремлении связать с практическими задачами изучение каждого раздела школьной математики, даже если это нарушало стройность и систематичность изложения.
А как вы думаете, полезно ли в старших классах показывать связь математики с практикой? Повышает ли это мотивацию? Углубляет ли знания?
— Ссылка:
Единство математики | Колмогоров А. Н. | Издательство МЦНМО
RB
/tr ru uz чел, ну это бан
M
/tr ru uz чел, ну это бан
odam, bu taqiq
М

Кто может помочь за плату?
V
odam, bu taqiq

Р
ы/се/се и тоже никогда не изучал высшую математику
Дока мб?
IS
Дока мб?
Не, я же удалил
Р
Не, я же удалил
Так установи
RB
Иск держись
IS
Иск держись
🦾
СМ
ну вот, теперь штаны в подливе
NK
📢 Репост из группы Абитуриенты мехмата МГУ:
Уважаемые абитуриенты и их родители!
В воскресенье 28 февраля 2021 года МГУ имени М. В. Ломоносова проводит День открытых дверей в формате онлайн на сайте https://openday.msu.ru/. День открытых дверей будет в основном ориентирован на иностранных абитуриентов, но абитуриенты из России также могут участвовать.
С 12:00 Вы сможете посмотреть выступление ректора МГУ академика РАН В. А. Садовничего и познакомиться с общей информацией об университете и поступлении.
С 13:00 на сайте будут доступны страницы факультетов МГУ, в том числе механико-математического факультета. На странице факультета вы сможете ознакомиться со следующими материалами:
- интервью с деканом факультета членом-корреспондентом РАН А. И. Шафаревичем;
- презентация с основной информацией о факультете;
- виртуальный тур по факультету.
В 14:30 начнётся онлайн-сессия механико-математического факультета для абитуриентов и их родителей (на платформе Zoom). Ссылка для подключения будет размещена здесь перед началом сессии. Запись сессии будет впоследствии размещена на нашем YouTube-канале для школьников и абитуриентов: https://www.youtube.com/channel/UCCJv7Ew5Z8UXtNb22YpLmMQ
— Ссылка:
День открытых дверей МГУ им. Ломоносова
Уважаемые абитуриенты и их родители!
В воскресенье 28 февраля 2021 года МГУ имени М. В. Ломоносова проводит День открытых дверей в формате онлайн на сайте https://openday.msu.ru/. День открытых дверей будет в основном ориентирован на иностранных абитуриентов, но абитуриенты из России также могут участвовать.
С 12:00 Вы сможете посмотреть выступление ректора МГУ академика РАН В. А. Садовничего и познакомиться с общей информацией об университете и поступлении.
С 13:00 на сайте будут доступны страницы факультетов МГУ, в том числе механико-математического факультета. На странице факультета вы сможете ознакомиться со следующими материалами:
- интервью с деканом факультета членом-корреспондентом РАН А. И. Шафаревичем;
- презентация с основной информацией о факультете;
- виртуальный тур по факультету.
В 14:30 начнётся онлайн-сессия механико-математического факультета для абитуриентов и их родителей (на платформе Zoom). Ссылка для подключения будет размещена здесь перед началом сессии. Запись сессии будет впоследствии размещена на нашем YouTube-канале для школьников и абитуриентов: https://www.youtube.com/channel/UCCJv7Ew5Z8UXtNb22YpLmMQ
— Ссылка:
День открытых дверей МГУ им. Ломоносова