Где этот тип, который «ГО БУХАТЬ».

За O(logn) надо, чтоб в Я попасть

Это прокол конечно.

Хотя нет, никакого прокола. Я не переворачиваю строки...Я ПЕРЕВОРАЧИВАЮ ИГРУ.

а тинек за константу(

Если в питоне без доп памяти сделаешь, то попадёшь

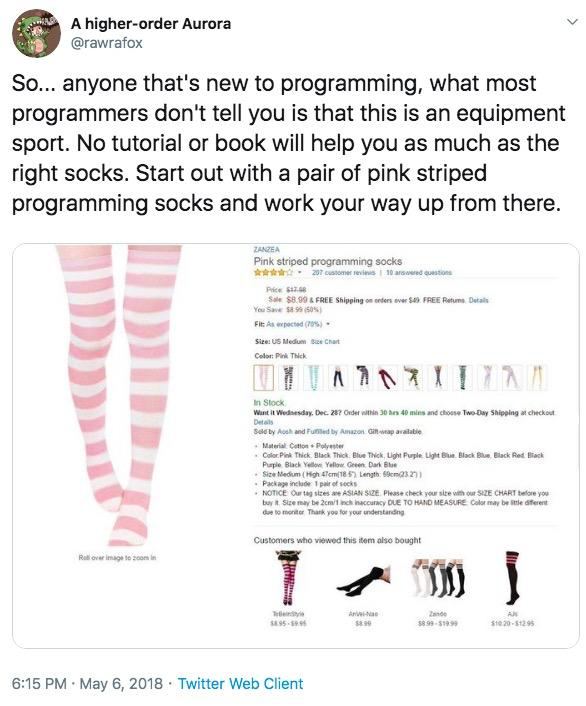
Что? Питон? Простите, но я такое не ношу.

*с придыханием* Но хотел бы...

Прими себя таким, какой ты есть

Текст в комментариях к оригинальному посту

📢 Репост пользователя Алексей Канель-Белов:

Dear Colleagues,

Allow me to highlight several questions which appear after
Mehdi Golafshan's talk; in my opinion, this should be related to
our work in progress with Nikolai Germanovich Moshchevitin.

Please comment and add your questions.

The talk was about Sturm's words and discrete dynamics.
We consider words in some finite alphabet which satisfy certain
properties < Mehdi, please give exact definitions> concerning their
factors.

One of the key example was related to the golden ratio \alpha:
y= \alpha x

We study this line propagating from (0,0) for x>0,
and write down a sequence of 0 and 1 any time it crosses
the horizontal /resp. vertical line y\in Z (resp., x\in Z).

Question 1. What will happen if we consider
z= \alpha x, y= \beta x for different irrational \alpha, \beta?
How are ergodic sequences related to the problem we
study with N.G.Moshchevitin?

[In our work we consider approximation of several
independent irrational numbers by rational numbers
with bounded denomiators; we look at possible permutations;
here we look at sequences of words in some alphabet;
how are they related to permut
]

Question 2. What about approximating an "irrational"
2-plane by rational 2-planes? There are results by Schmidt;
Nikolai Germanovich can formulate them more exactly.
Can we define any "ergodic" properties corresponding to
2-planes in R^{4} (or any other dimension)?

Question 3. How is this theory related to the dynamics
if we take a geodesic line for a hyperbolic surface of genus
g glued from a (4g)-gon? We'll have 2g letters; how to describe
the set of words one can obtain this way? How are they
related to Sturm's word? How are they related to Gromov's work?

Question 4. a) What if we consider several "irrational"
geodesic lines? Can we get a presentation of the braid group
acting on the words?
b) Can we get representations of "non-closed braids"
by using some averaging;
maybe, we may tackle some asymptotic invariants like
Arnold's asymptotic linking number
c) Possibly, we can invent "non-closed analogues" of other
groups, not necessarily braid groups.

Question 5. How is the above theory related to the
distribution of primes?

Please upload all necessary papers: Belov-Mehdi-Mitrofanov,
Moshchevitin-Kahn etc.

Поселили в гз. Подскажите как лучше сымитировать возгорание проводки чтобы комнату после пожара побыстрее отремонтировали или дали другую. Спасибо

Не место красит человека

Сам отремонтируй

А что

А человек место

За свой счёт

А на следующий год тебя селят в другую

Северный поток 2 и санкционный цугцванг

Северный поток 2, который уже несколько лет является предметом жарких юридико-политических дебатов между США, ЕС и Россией, судя по всему таки будет достроен несмотря на все санкционные усилия США.
Так несмотря на отказ российской частной компании предоставить своё судно для прокладки трубопровода, Россия решила перегнать необходимые суда с Тихого океана в сопровождении военных судов, что явно говорит о решимости закончить трубопровод в кратчайшие сроки.

Сам по себе Северный поток, как первый так и второй, могут рассматриваться исходя из двух парадигм: диверсификации и монополизации.
Для России наличие наибольшего числа путей поставки газа из России в Европу является способом диверсификации, который позволяет избавиться от рисков конкретной страны транзитера, будь то Украина, Белоруссия, Турция или Германия. Изначально избыточная мощность каждого газопровода позволяет свободно перемещать объём поставок между ними , а потенциальная возможность полной остановки поставок может лишить страну транзитера прибыли. Более того, в случае повышения спроса в Европе указанные мощности могут быть быстро заполнены для увеличения доля России на газовом рынке Европы, что так же даст России больше политического влияния.

Однако, такая диверсификацией и возможность резко увеличить поставки так же ведёт к доминированию России в Европе. Опасаясь этого, США решили действовать двумя путями: (1) постройкой терминалов СПГ в Европе и (2) санкциями.
Однако, строительство инфраструктур для СПГ требует больших разовых вложений, а сам СПГ оказался значительно дороже российского. Такое положение было достигнуто за счет монополии Газпрома на экспорт газа, что в свою очередь позволило, за счет централизованного переговорного процесса предоставлять значительные скидки за крупные оптовые контракты, которые не возможны на рынке СПГ, где доминируют множество игроков не способные к координации и совместным действиям. А европейские элиты, хоть и волнуются о российском влиянии, также озабочены экономическим ростом , который требует как можно более дешевых цен на энергоресурсы, особенно в таких индустриально развитых странах как Германия.

Санкционная политика же хоть и имела на начальных этапах некоторый успех, быстро зашла в тупик. К настоящему времени США использовали уже почти весь доступный санкционный арсенал, однако так и не достигли главного – остановки строительства и отказа европейских потребителей от российского газа.
Следующий логический шаг это наложить санкции на всех строителей Северного потока 2. Однако проблема состоит в том, что это не только Газпром, но и германские Uniper и Wintershall Dea, австрийская OMV, французская Engie и англо-голландская Shell. Опыт Русала, в свою очередь, показал, что-то современной глобальной экономике невозможно наложить санкции на крупного международного игрока и не навредить мировому рынку.

Однако, даже если США и решится пойти не такой рискованный шаг, это также может принести России долгосрочную, пусть и не экономическую, но политическую выгоду. Так это лишь усилит размолвку между США и ЕС, однако, что более важно, даст огромный толчок европейскому механизму обхода санкций введённый так называемым Блокирующим Статутом (Регламент ЕС 2271/96), который запрещает компаниям из ЕС следовать иностранным правовым актам и судебным решениям и позволяет таким компаниям взыскивать убытки от санкций с компаний, подчиняющихся таким санкциям, в судах ЕС. И хотя, необходимо признать, что данный механизм пока ещё со скрипом работает в отношении Ирана, текущая санкционная угроза в отношении газопровода в Европе и угроза санкций в отношении европейских компаний как ничто другое способствует его усилению.

Данная ситуация как нельзя лучше иллюстрирует закат американского величия, когда растеряв значительную часть власти и престижа и все ещё пытаясь решать вопросы силой как раньше, страна загоняет себя в цугцванг, где любой следующих шаг ведёт к поражению и самый лучший выход – ничего не делать, но это увы невозможно.

Всех американцев накол