i
Size: a a a
2020 March 08
Всем привет
ZP
Бесконечная площадь δ функции, может быть?
нет
2020 March 09
{
Глупый вопрос, правда ли, что если h = fg гомеоморф, то g гомеом?
A
R -> R^2 -> R?
{
R -> R^2 -> R?
да, забыл условие f гомотопно константе, вообще мб я не понимаю заключения, в общем, как доказать, что если отображение корасслоение (cofiber), то оно вложение(embedding)?
lg
Упр. Если отображение Х to У cofiber, то у отображения Cyl(f) to X x I есть сечение
{
Упр. Если отображение Х to У cofiber, то у отображения Cyl(f) to X x I есть сечение
Всмсл у любого отображения из цилиндра?
lg
Не, вполне конкретное отображение, заданное отображение X to Y. Правда там опечатка, я имел в виду Cyl(f) to Y x I
{
Не, вполне конкретное отображение, заданное отображение X to Y. Правда там опечатка, я имел в виду Cyl(f) to Y x I
(Я думаю, что ты имеешь в виду вот такое отображение)
Cyl(f) —> Y x I : (x, t) —> (f(x), t), y —> (y, 0) (пусть у цилиндра Y приклеено к X x {0})
Можно продолжить вложения X x I —> Cyl(f), Y —> Cyl(f) до отображения Y x I —> Cyl(f), но будет ли это сечением? (других разумных отображений не удаётся придумать)
Cyl(f) —> Y x I : (x, t) —> (f(x), t), y —> (y, 0) (пусть у цилиндра Y приклеено к X x {0})
Можно продолжить вложения X x I —> Cyl(f), Y —> Cyl(f) до отображения Y x I —> Cyl(f), но будет ли это сечением? (других разумных отображений не удаётся придумать)
2020 March 10
i
Математики у
ツダ
математики у
S
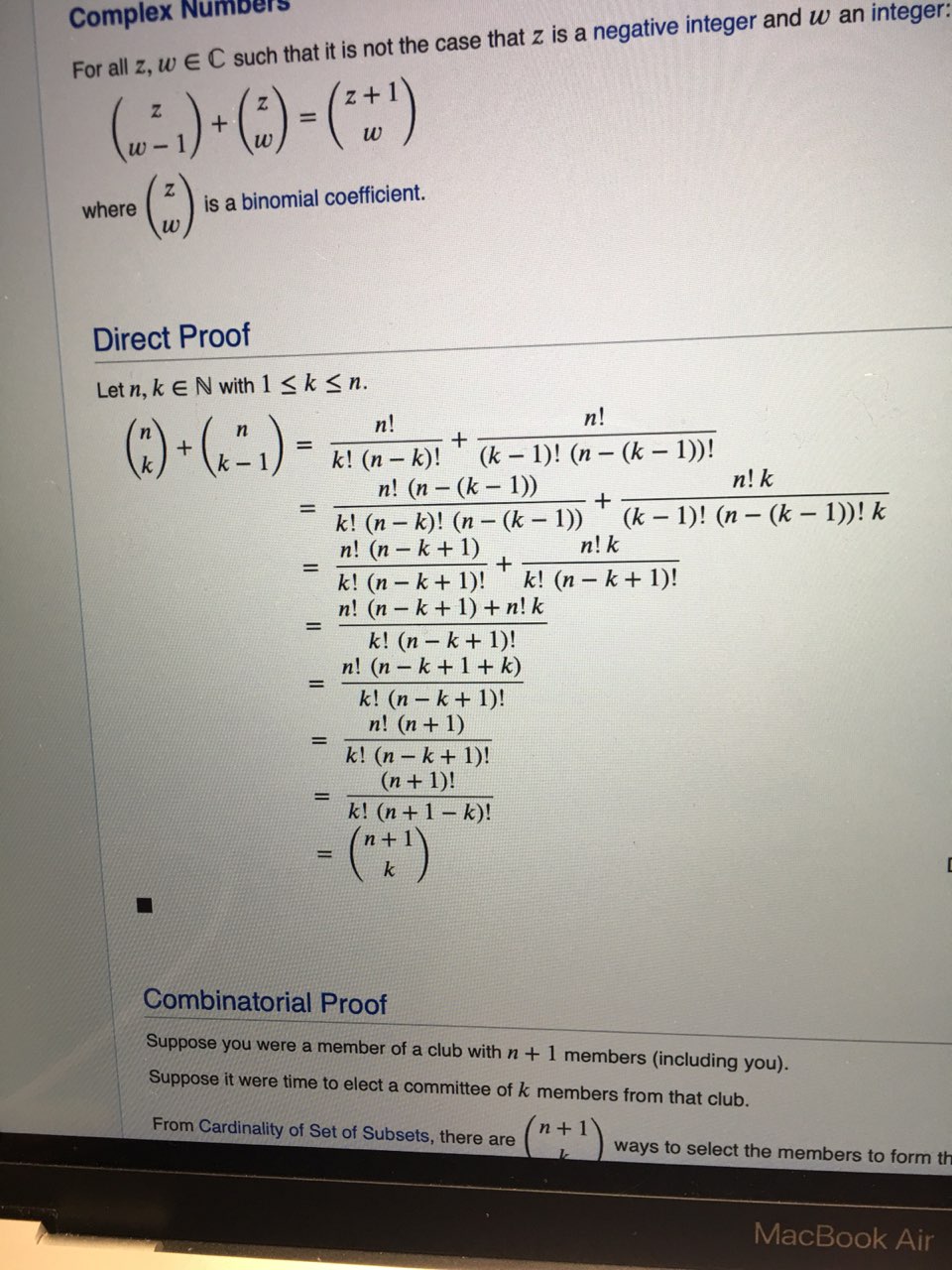
привет всем, только не бейте сильно! Скажите как доказываются биномиальные коэффициенты, например, (n k) + (n k+1) = (n+1 k+1)
мне непонятно, прежде всего, как получается общий знаменатель из
n!/(k!*(n-k)! + n!/((k+1)!*(n-k-1)!) =
(k+1)!*(n-k)! + (k+1)! * (n-k)! (общий знаменатель, числитель я не указал)
мне непонятно, прежде всего, как получается общий знаменатель из
n!/(k!*(n-k)! + n!/((k+1)!*(n-k-1)!) =
(k+1)!*(n-k)! + (k+1)! * (n-k)! (общий знаменатель, числитель я не указал)
DK
S
привет всем, только не бейте сильно! Скажите как доказываются биномиальные коэффициенты, например, (n k) + (n k+1) = (n+1 k+1)
мне непонятно, прежде всего, как получается общий знаменатель из
n!/(k!*(n-k)! + n!/((k+1)!*(n-k-1)!) =
(k+1)!*(n-k)! + (k+1)! * (n-k)! (общий знаменатель, числитель я не указал)
мне непонятно, прежде всего, как получается общий знаменатель из
n!/(k!*(n-k)! + n!/((k+1)!*(n-k-1)!) =
(k+1)!*(n-k)! + (k+1)! * (n-k)! (общий знаменатель, числитель я не указал)
забей
PS
S
привет всем, только не бейте сильно! Скажите как доказываются биномиальные коэффициенты, например, (n k) + (n k+1) = (n+1 k+1)
мне непонятно, прежде всего, как получается общий знаменатель из
n!/(k!*(n-k)! + n!/((k+1)!*(n-k-1)!) =
(k+1)!*(n-k)! + (k+1)! * (n-k)! (общий знаменатель, числитель я не указал)
мне непонятно, прежде всего, как получается общий знаменатель из
n!/(k!*(n-k)! + n!/((k+1)!*(n-k-1)!) =
(k+1)!*(n-k)! + (k+1)! * (n-k)! (общий знаменатель, числитель я не указал)
1. Комбинаторно
2. Из бинома Ньютона
3. Явно исходя из формулы
2. Из бинома Ньютона
3. Явно исходя из формулы
S
S
спасибо, мне просто непонятен принцип общего знаменателя во второй строке
PS
Если долго на него смотреть, можно понять
Ж
S
привет всем, только не бейте сильно! Скажите как доказываются биномиальные коэффициенты, например, (n k) + (n k+1) = (n+1 k+1)
мне непонятно, прежде всего, как получается общий знаменатель из
n!/(k!*(n-k)! + n!/((k+1)!*(n-k-1)!) =
(k+1)!*(n-k)! + (k+1)! * (n-k)! (общий знаменатель, числитель я не указал)
мне непонятно, прежде всего, как получается общий знаменатель из
n!/(k!*(n-k)! + n!/((k+1)!*(n-k-1)!) =
(k+1)!*(n-k)! + (k+1)! * (n-k)! (общий знаменатель, числитель я не указал)
Рассмотрим n пронумерованных шаров. Зафиксируем какой то конкретный шар. Попробуем посчитать количество комбинаций длины k которые включают этот шар и которые не включают. Сумма этих двух наборов комбинаций даст (n k)
DK
Если долго на него смотреть, можно понять
долго смотрел в лицо твоей матери
DK
и случайно кончил на нее



