З
Size: a a a
2021 May 28
спасибо
З
я тут полистал этот учебник
З
там какие-то матрицы
З
матан
З
видимо ранновато
КС
Так конечно, это для студентов.
КС
Для шкилы рекомендую пятитомник мякишева. На канале он тоже есть.
З
да, надо было прочитать предисловие
З
блин он огромный
З
но всё же хороший
EM
EM
Você por aqui ?
EL
Brasileiro existe em todo lugar
D
Ребят, помогите с задачей:
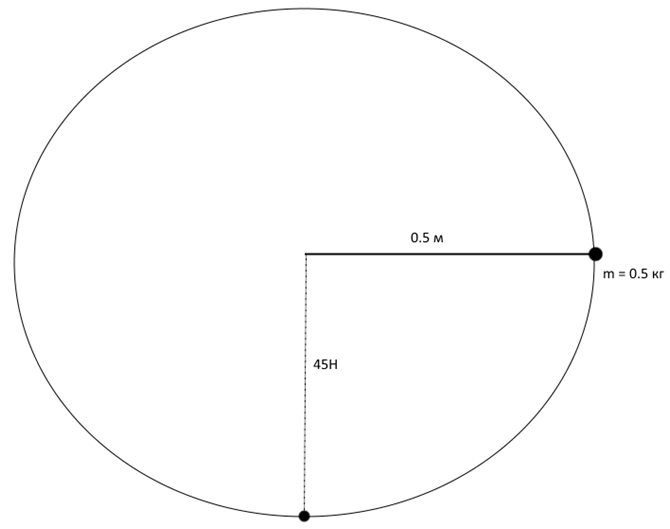
Тело, массой 0.5 кг закреплённое на конце стержня длиной 0.5 м, равномерно вращается в вертикальной плоскости. Натяжение в нижней точке окружности 45 Н. На какую высоту h (в метрах), относительно нижней точки подлетит тело, если оно отрывается от стержня в тот момент, когда его скорость направлена вертикально вверх?
Мои догадки:
1) Cкорость тела направлена вертикально в тот момент, когда тело находится в одном из двух средних положений.
2) При отрыве от стержня, тело полетит вертикально вверх.
3) Задачу можно рассмотреть как совокупность двух более простых подзадач. Первая подзадача - найти центростремительное ускорение тела в точке отрыва через второй закон ньютона. Вторая подзадача - найдя ускорение, можно по формуле центростремительного ускорения выразить скорость, затем подставить её в уравнение полёта тела брошенного вертикально вверх.
4) Если для верхней точки окружности в проекции на ось y закон ньютона имеет вид: mg + T1 = ma, а для нижней точки окружности закон ньютона имеет вид: T2 - mg = ma (где a - это центростремительное ускорение, а T1 и T2 - сила натяжения стержней), то будет ли корректен таков закон ньютона для произвольной точки движения по окружности: T3 - mg*cos(alpha) = ma, где alpha - угол между вертикальным направлением вниз и стержнем, если это так, то в данной точке сила тяжести зануляется. И ещё центростремительное ускорение в разные моменты будет разное.
5) Вот примерно поясняющий рисунок.
Тело, массой 0.5 кг закреплённое на конце стержня длиной 0.5 м, равномерно вращается в вертикальной плоскости. Натяжение в нижней точке окружности 45 Н. На какую высоту h (в метрах), относительно нижней точки подлетит тело, если оно отрывается от стержня в тот момент, когда его скорость направлена вертикально вверх?
Мои догадки:
1) Cкорость тела направлена вертикально в тот момент, когда тело находится в одном из двух средних положений.
2) При отрыве от стержня, тело полетит вертикально вверх.
3) Задачу можно рассмотреть как совокупность двух более простых подзадач. Первая подзадача - найти центростремительное ускорение тела в точке отрыва через второй закон ньютона. Вторая подзадача - найдя ускорение, можно по формуле центростремительного ускорения выразить скорость, затем подставить её в уравнение полёта тела брошенного вертикально вверх.
4) Если для верхней точки окружности в проекции на ось y закон ньютона имеет вид: mg + T1 = ma, а для нижней точки окружности закон ньютона имеет вид: T2 - mg = ma (где a - это центростремительное ускорение, а T1 и T2 - сила натяжения стержней), то будет ли корректен таков закон ньютона для произвольной точки движения по окружности: T3 - mg*cos(alpha) = ma, где alpha - угол между вертикальным направлением вниз и стержнем, если это так, то в данной точке сила тяжести зануляется. И ещё центростремительное ускорение в разные моменты будет разное.
5) Вот примерно поясняющий рисунок.
D
Что делать дальше и верно ли это всё сказанное
C
В нижнем точке използуя 2 закон Нютона можнш найти ускорение (ma=T-mg) използуя исползуя ускорение можеш найти скорость а потом высота будет V*t-gt²/2
WA
Люде, вот вы тут думаю любите решать задачи. А у меня с этим проблемы. С решением задач по программированию (например на степике). Как думаете, изучение логики поможет мне с нешением задач?
WA
Сори за офтоп
И
Мне кажется да, сам на степике решаю, большинство задач именно на логику