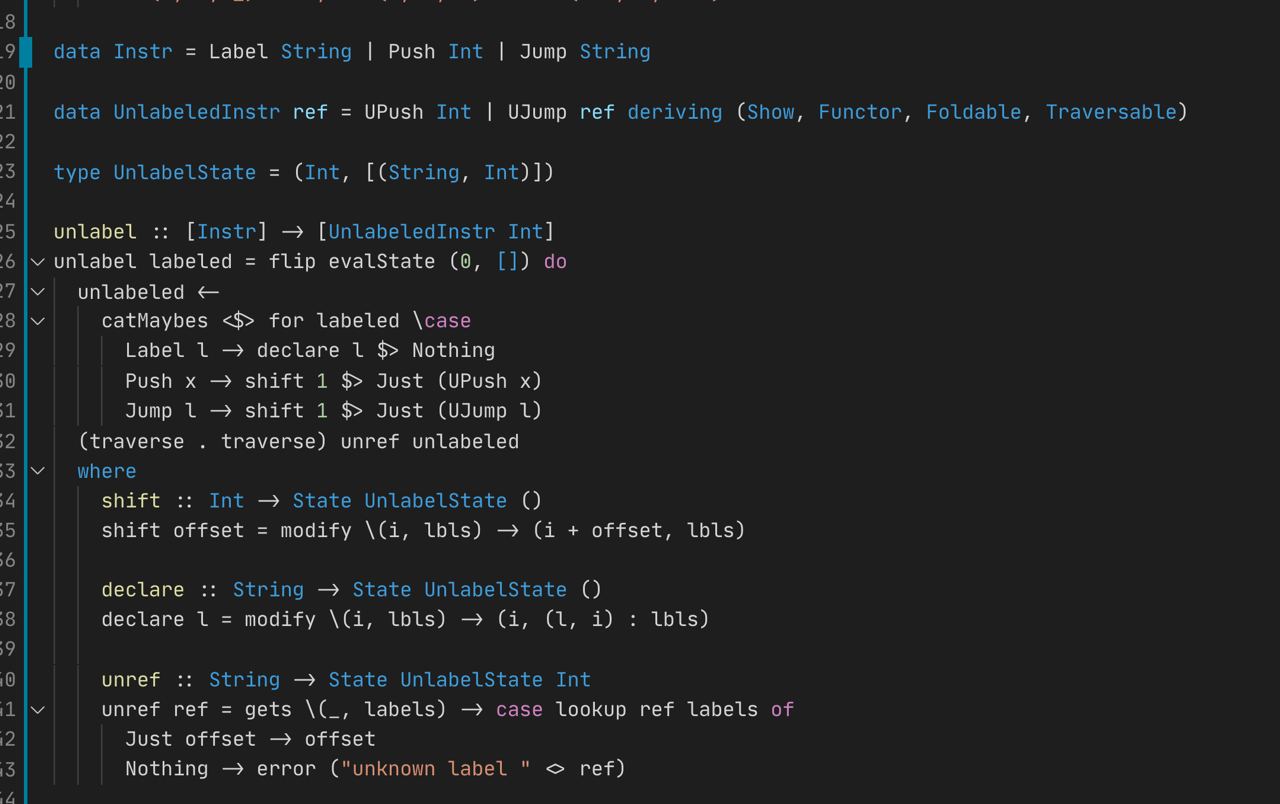
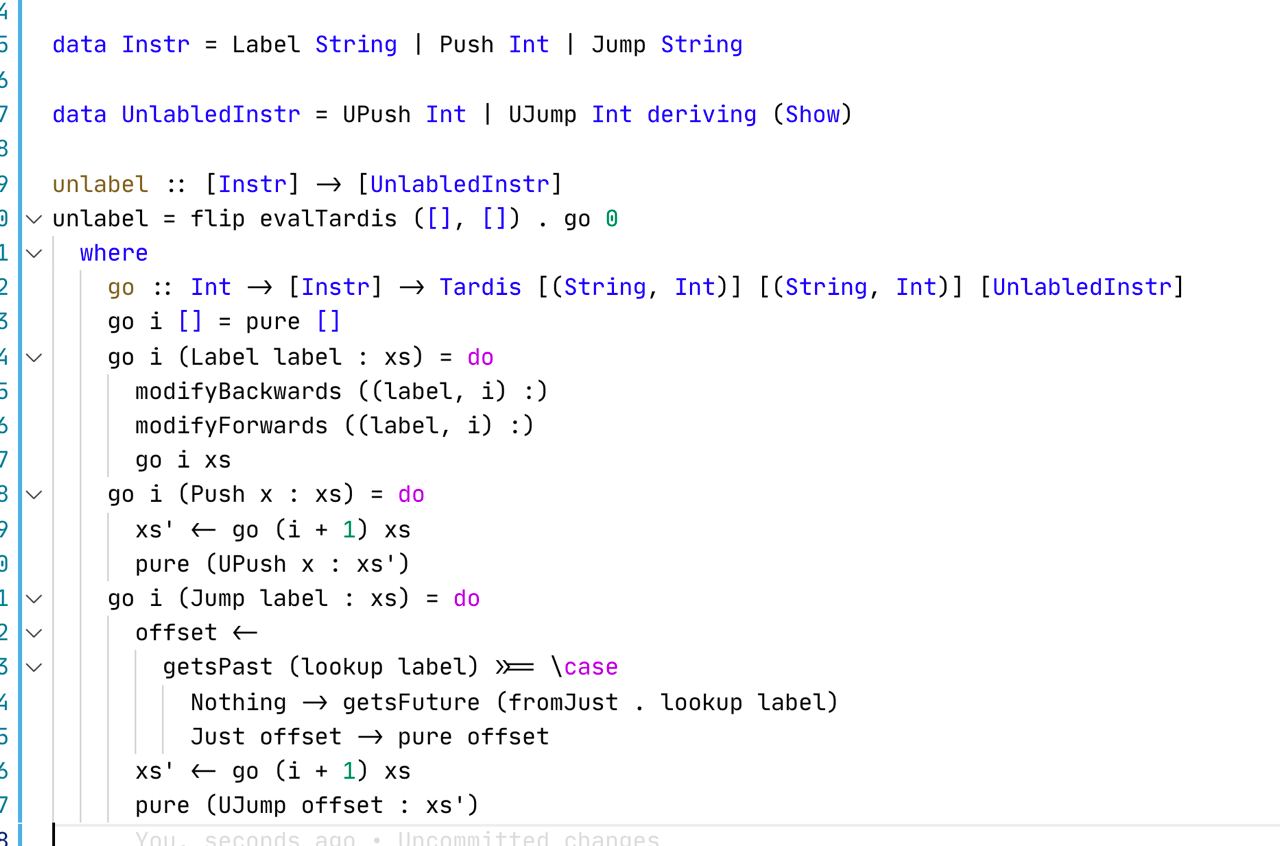
к
data Free f a
= Pure a
| Free (f (Free f a))
deriving (Functor)
instance Functor f => Applicative (Free f) where
pure = Pure
(<*>) = ap
instance Functor f => Monad (Free f) where
Pure x >>= f = f x
Free m >>= f = Free (fmap (>>= f) m)
data MyIOT a
= Print Text a
| GetLine (Text -> a)
deriving (Functor)
myPrint :: Text -> Free MyIOT ()
myPrint str = Free (Print str (Pure ()))
myGetLine :: Free MyIOT Text
myGetLine = Free (GetLine Pure)
foldPrints :: Free MyIOT a -> Free MyIOT a
foldPrints (Free (Print a (Free (Print b next)))) = foldPrints $ Free (Print (a <> "\n" <> b) next)
foldPrints (Free (Print a next)) = Free (Print a (foldPrints next))
foldPrints (Free (GetLine next)) = Free (GetLine (foldPrints . next))
foldPrints (Pure x) = Pure x
alg :: MyIOT a -> IO a
alg (Print a next) = putStrLn ("output: " <> a) >> pure next
alg (GetLine next) = next <$> (putStr "input: " >> getLine)
runFree :: Monad m => (forall x. f x -> m x) -> Free f a -> m a
runFree f (Pure x) = pure x
runFree f (Free m) = f m >>= runFree f
main2 :: IO ()
main2 = runFree alg $ foldPrints do
myPrint "Hello"
myPrint "enter your name:"
name <- myGetLine
myPrint "your name is"
myPrint name
с оптимизацией
*Main> main2
output: Hello
enter your name:
input: kana
output: your name is
kanaбез оптимизации
*Main> main2
output: Hello
output: enter your name:
input: kana
output: your name is
output: kana