ТТ
Size: a a a
2021 February 19
JS
Ксж это тогда всеобщая ошибка. Втч производителей железа (
да, и от неё не изюавиться, можно только пытаться минимизировать ущерб
AL
Да :-)
Привести док-во?)
Ну и другие свойства есть. Бине-Коши. Ну или более тривиальные, вроде изменения знака или равенства нулю при линейной зависимости строк/столбцов
Привести док-во?)
Ну и другие свойства есть. Бине-Коши. Ну или более тривиальные, вроде изменения знака или равенства нулю при линейной зависимости строк/столбцов
Думаю, доказательство использует ассоциативность умножения чисел
AL
Теорема тарского нам как бы намекает что равенство вещественных чисел undecidable
ТТ
Теорема тарского нам как бы намекает что равенство вещественных чисел undecidable
А можно чуть подробней или ссылку?
MK
Теорема тарского нам как бы намекает что равенство вещественных чисел undecidable
для НАСТОЯЩИХ вещественных чисел
MK
которых в компьютерах не бывает
JS
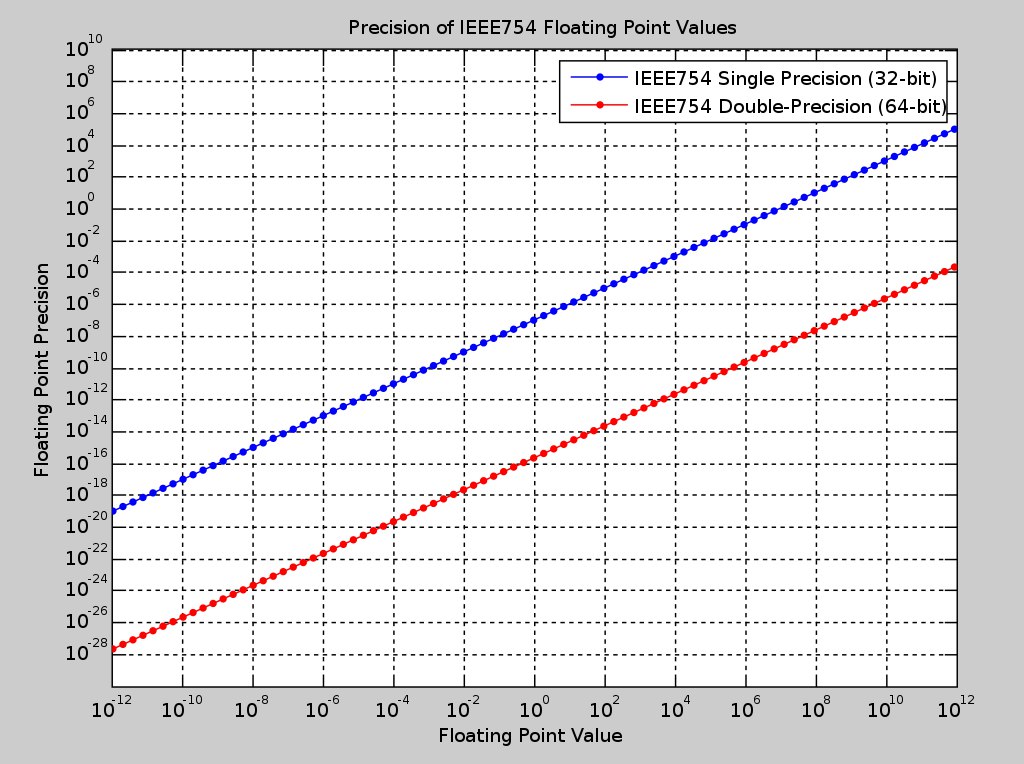
ух ты, float80 aka long double aka ten byte нет в стандарте https://en.wikipedia.org/wiki/IEEE_754
JS
кстати, ко грехам IEEE 754 стоит добавить грехи реализации в 8087, когда результат цепочки действий зависит от того, вставил ли компилятор промежуточную выгрузку из сопроцессора (с точностью в 80 бит) в основную память размером в 32 или 64 бита
AL
для НАСТОЯЩИХ вещественных чисел
Ну разумеется; а ненастоящие будут иметь понятно какие проблемы
AL
ух ты, float80 aka long double aka ten byte нет в стандарте https://en.wikipedia.org/wiki/IEEE_754
Есть, называется extended precision
AL
То есть там конечно 79 бит, но всем понятно
AL
А можно чуть подробней или ссылку?
Ну про равенство это совсем тривиально; чуть менее тривиально что нельзя сложить два вещественных числа: первая же цифра результата зависит от знания бесконечного числа цифр слагаемых
ТТ
Ну про равенство это совсем тривиально; чуть менее тривиально что нельзя сложить два вещественных числа: первая же цифра результата зависит от знания бесконечного числа цифр слагаемых
Да, уже почитал, пасибо )
ТТ
Но у нас то числа ограниченной точности 😉
То, о чём @maksbotan говорил.
То, о чём @maksbotan говорил.
A
Теорема тарского нам как бы намекает что равенство вещественных чисел undecidable