Size: a a a
2017 March 02

40. К кусочку ткани размером 3×3 к центральной клеточке приклеен кубик 1×1×1. Ткань можно разрезать, но нельзя отрезать кусочки. Можно ли завернуть весь кубик в эту ткань?
2017 March 03

41. Барон Мюнхгаузен утверждает, что ему удалось составить некоторый прямоугольник из нескольких подобных между собой непрямоугольных треугольников. Можно ли ему верить?
Автор: А. Федотов
Источник: Турнир городов 1997/98
Автор: А. Федотов
Источник: Турнир городов 1997/98
2017 March 04

Решение задачи 40

Нужно ли публиковать задачки в выходные?
Да, хотим – 93
👍👍👍👍👍👍👍 59%
Не важно – 37
👍👍👍 24%
Нет, и так много – 27
👍👍 17%
👥 157 people voted so far.
Да, хотим – 93
👍👍👍👍👍👍👍 59%
Не важно – 37
👍👍👍 24%
Нет, и так много – 27
👍👍 17%
👥 157 people voted so far.
2017 March 06

Добрый день всем! Сегодня с вами снова я, Константин Кноп. И у нас в меню снова комбинаторная геометрия. Помните задачу о покрытии треугольника тремя квадратами? Сегодня — «задача наоборот»:
42. Найдите как можно больший квадрат, который можно полностью покрыть (с наложениями, но без «дырок») четырьмя правильными треугольниками со стороной 1.
42. Найдите как можно больший квадрат, который можно полностью покрыть (с наложениями, но без «дырок») четырьмя правильными треугольниками со стороной 1.

Если расположить треугольники так, как показано на рисунке, они покрывают квадрат со стороной 1.5(sqrt(3)-1). Примерно 1.098
2017 March 07

Источник: http://www2.stetson.edu/~efriedma/tricosqu/
Максимальность этого результата не доказана, но с 2002 года его никто не улучшил, так что определенные гарантии есть.
Максимальность этого результата не доказана, но с 2002 года его никто не улучшил, так что определенные гарантии есть.

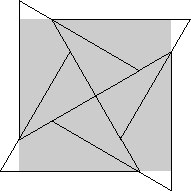
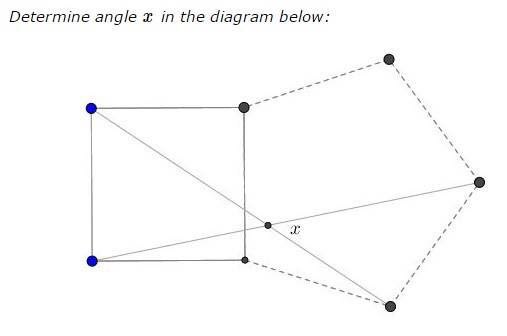
43. Найдите угол x на рисунке

Ответ на задачу 43: 45°. А решение будет уже завтра...
2017 March 08

Сегодня задача на построение. ;-)
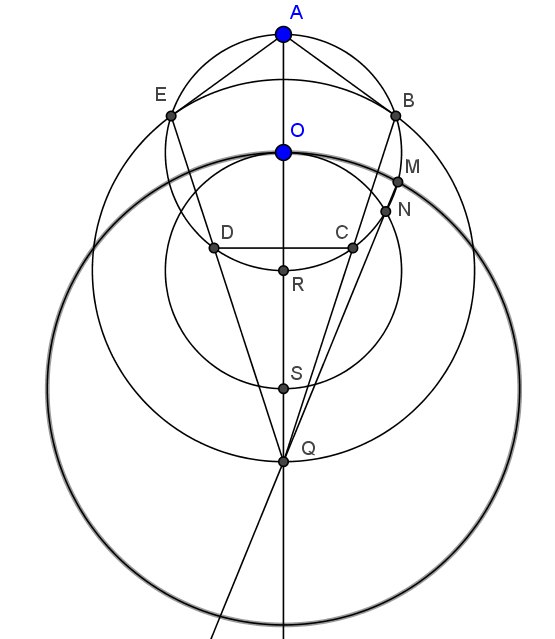
44. Дана окружность с центром O. Вписать в нее правильный пятиугольник, проведя не более 10 линий: 3 окружности и 7 прямых.
44. Дана окружность с центром O. Вписать в нее правильный пятиугольник, проведя не более 10 линий: 3 окружности и 7 прямых.

Решение задачи 44. Сначала проводим прямую AO, затем окружности с центрами R и S, проходящие через точку О, потом прямую MN. В пересечении с AO эта прямая даёт точку Q, а окружность (R, RQ) даёт вершины B и E. Дальше остаётся только построить стороны пятиугольника — AB, BQ, QE, EA, и соединить между собой получившиеся точки C и D.

Всех прекрасных дам, читающих наш канал, поздравляю с праздником 8 марта.
2017 March 09

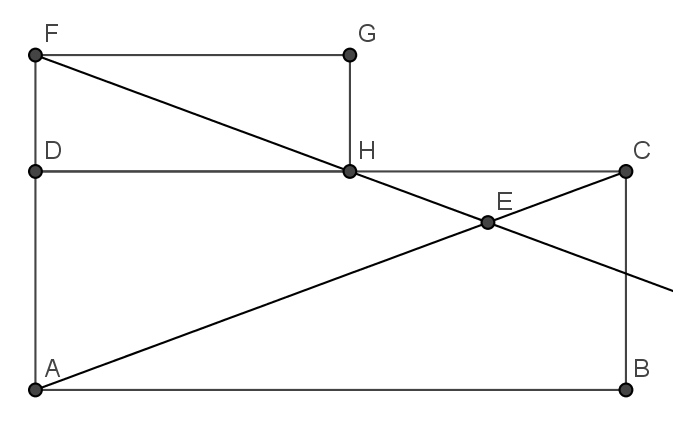
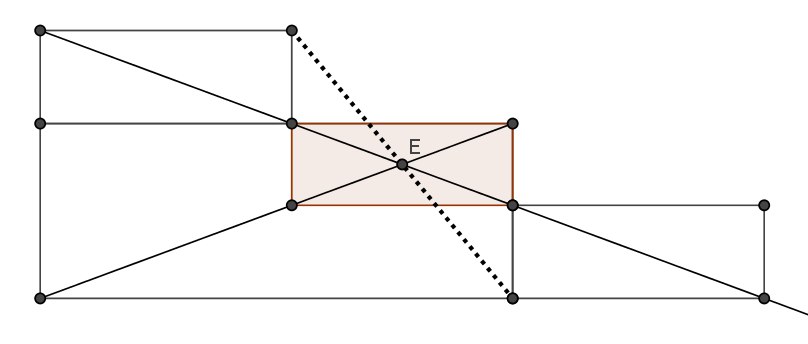
45. Даны два подобных прямоугольника ABCD и DHGF. Диагонали AC и FH пересекаются в точке E. Докажите, что E — середина BG.