Ну, относительно граветцев есть вопрос - жили ли они в районе современной Вены на пике оледенения, или они сначала ушли, а потом их уже неолитические потомки обратно пришли?

Ну, в Мезозое его предки уже были наземными млекопитающими и, скорее всего, в море не жили.

Да и вряд ли он произошëл от местных приматов (если они вообще там жили), вероятнее всего, таки вышел из Африки как и остальные.

Он с одноклеточных начинал

Лукич

Карта рельефа Альп от Google.

📖 Географ

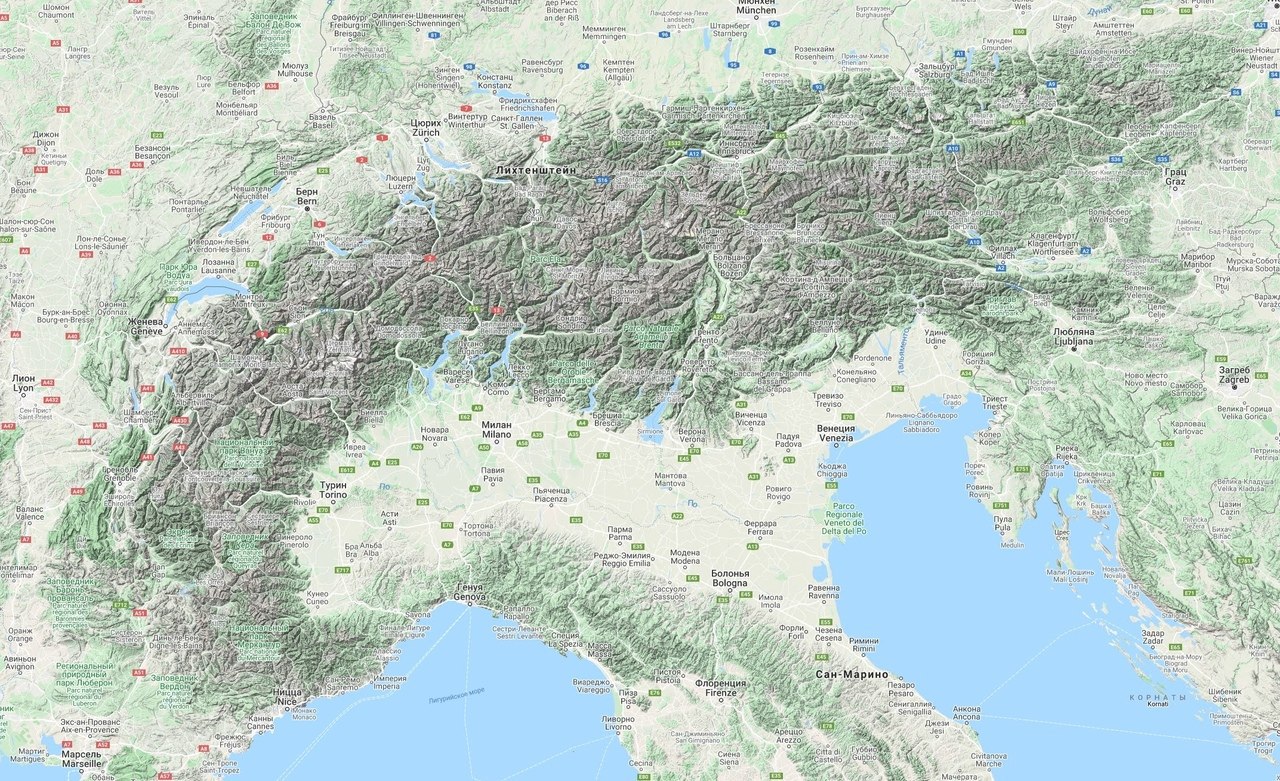
Где Шамони?

Альпы все под ледником были? По маковку?

https://zen.yandex.ru/media/chsdozor/ploscad-prirodnyh-pojarov-prevysila-poltora-milliona-gektar-i-sostavila-1-mln-686-tysiach-i-18-ga-5efb3b3ec82484567e62c920
Площадь природных пожаров превысила полтора миллиона гектар и составила 1 млн 686 тысяч и 18 га.

Ну, прошлый год орали, еле заставили вроде исключить это "наблюдение", а нынче снова и опять, под шумок.

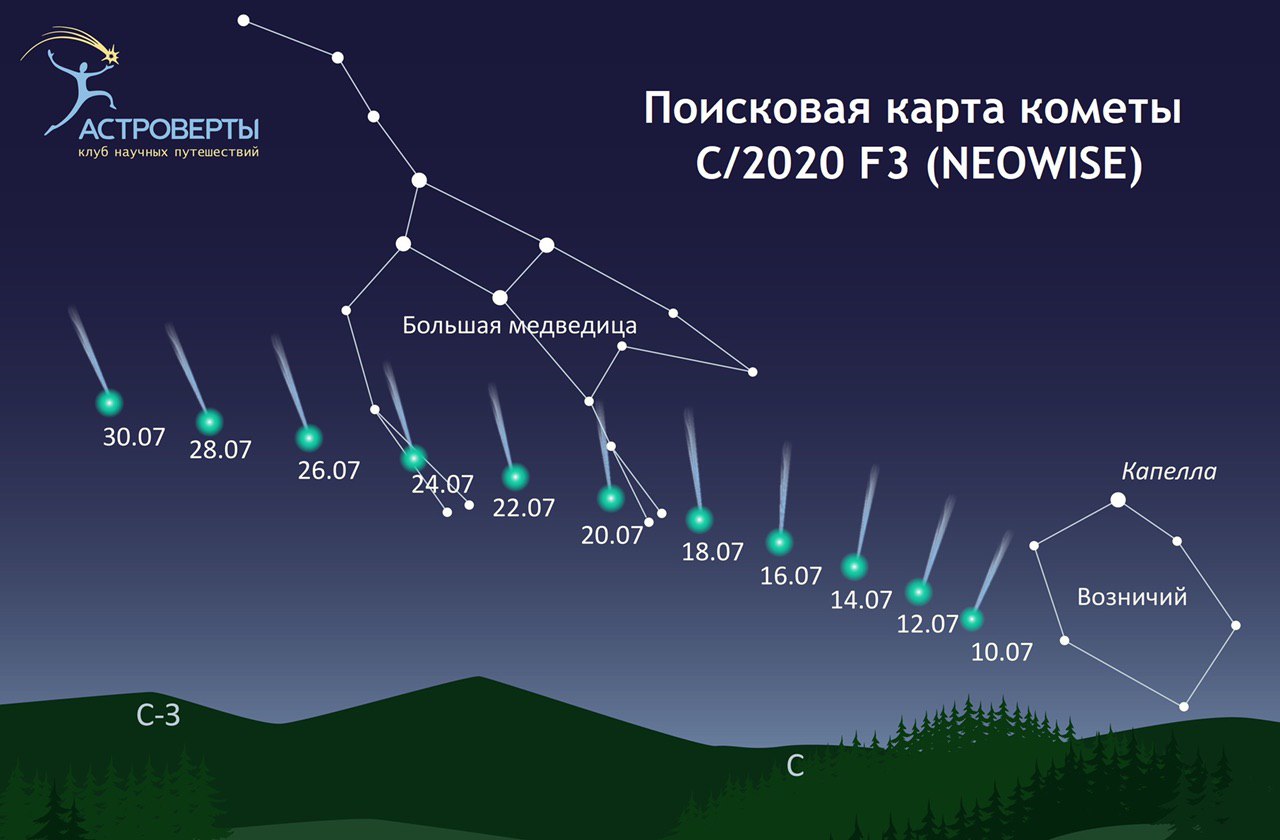
Отличная возможность увидеть редкую комету! Всем рекомендую такой опыт

Комета C/2020 F3 (NEOWISE) 3 июля пересечет орбиту Меркурия и окажется в 43 млн км от Солнца, после чего начнет удаляться от него и (если прогнозы оправдаются) 10 июля появится на предрассветном небе около созвездия Возничего с блеском порядка +1 зв. вел.

Наилучшие условия видимости сложатся около 20 июля, когда NEOWISE войдет в созвездие Б.Медведицы при блеске +3 зв.вел. Глазом она будет заметна как слабое пятнышко, но в бинокль, возможно, будет виден ее хвост! Так же, комета будет легко доступна для съемок на фотоаппараты с объективами.

Открытка @filippovakati

В Якутске появилась копия знаменитой шапокляк, которая не только достает соседей, но и технично уходит от ответственности. Бодрая бабка

Смешно)

Соседям явно не очень.

Да она везде уже в телефоне. Главное чтобы ее участковый терапевт это увидел. А то бывают такие, куча жалоб, охи ахи, а пока никто не видит велосипедами кидаются.

​Картографический экзерсис

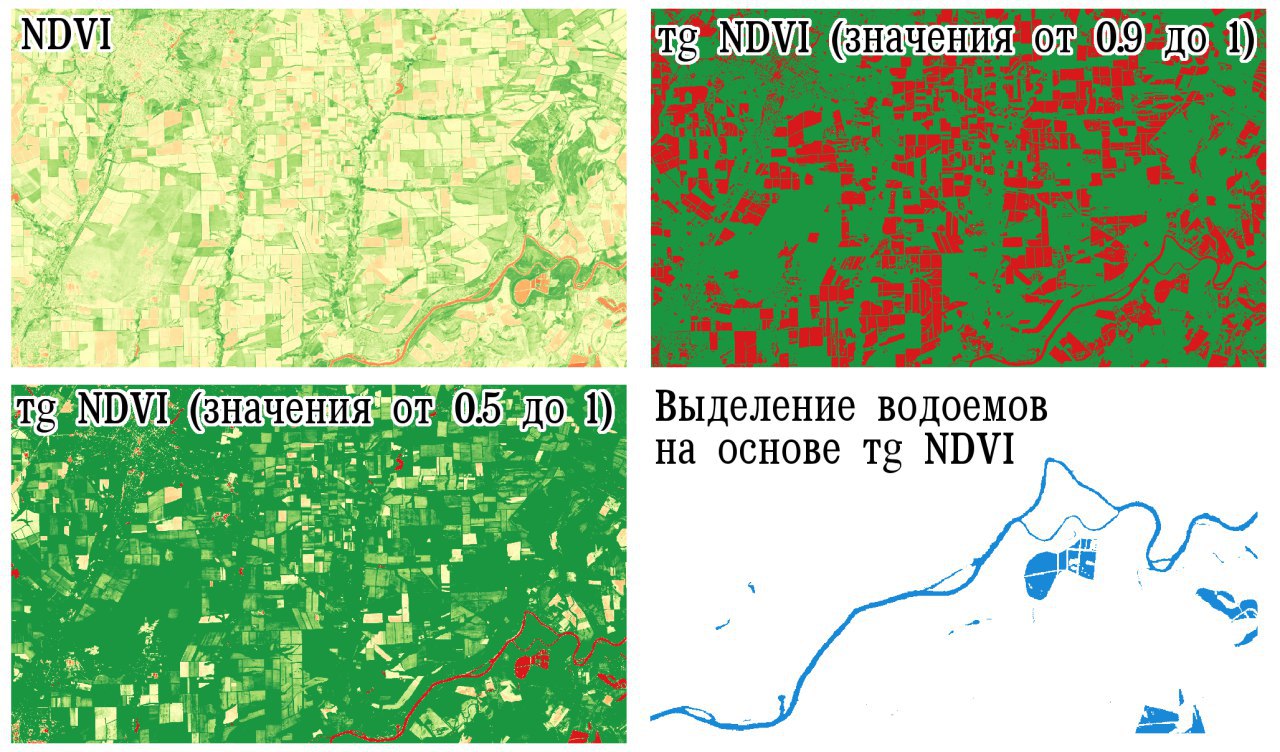
Нет ничего сексуальнее тригонометрии в необычных местах. Например, представление двумерного массива в качестве суммы квадратов синуса и косинуса. Это позволяет извлечь угол, который мало что дает, но невероятно притягивает. Или взять индекс NDVI. В конце семидесятых Ричардсон и Виганд предложили перпендикулярный вегетационный индекс - по сути бесполезная фигня, но какой полет мысли!

Или взять перпендикулярную раскраску слоя в гисах. Обычно одноканальные растры красят примитивно: малые значения красненьким, а большие зелененьким или наоборот. Но иногда имеет смысл одним цветом выделить краевые значения, а другим центральные. Сделать это можно разными способами, начиная от ручного задания диапазона, заканчивая вычислением модуля разницы текущего и среднего пикселя. Но все это так грубо, что даже противно. Другое дело - подключить тригонометрию.

Представьте, что значения яркости в канале соответствуют величине некоторого мифического угла. Сам этот угол пусть никого не интересует, важно лишь то, что в прямоугольном равнобедренном треугольнике оба острых угла равны сорока пяти градусам. Это значит, что нормализовав значения яркости к диапазону 0-90, мы получим пересечение графика синуса и косинуса яркости для значения 45. Следовательно, чем ближе значения яркости к медиане, тем ближе значения тангенса яркости к единице.

В практическом смысле это дает возможность выделять объекты со средними значениями. Например, поля на растре вегетационного индекса. Более того, немного поиграв с настройками диапазона отображения или добавив в расчеты побольше степеней, мы можем неплохо отсеивать объекты с резко отклоненными значениями, например водоемы.

Много ли это дает в реальной работе? Да почти ничего. Но боже мой, как же это сексуально.

Именно для этого в ГИС системах существует работа с растрами)

Привет из столицы нефтяников Татарстана