A
Size: a a a
2020 February 01
Ну да, вот так я это понимаю теперь... Т.е. равенство это вот просто символ с 3 св-вами, перечисленными выше и оно просто есть. Но как только мы укажем на конкретную категорию, то нужно будет объяснить что оно значит. Всем большое спасибо за объяснения!
Но дело в том, что почти никогда не указывают, подразумевая обычное равенство (у него эти свойства автоматически выполнены). Ну и да, в высших категориях появляются морфизмы между морфизмами, так что можно будет рассматривать изоморфные морфизмы, но это более сложная наука.
2020 February 02
МБ
Но дело в том, что почти никогда не указывают, подразумевая обычное равенство (у него эти свойства автоматически выполнены). Ну и да, в высших категориях появляются морфизмы между морфизмами, так что можно будет рассматривать изоморфные морфизмы, но это более сложная наука.
"Обычное" равенство тоже такое себе, нетривиальное понятие. Вот
2 = 2 -- это, вроде как, очевидно, а 2 + 2 = 4 -- уже не очень, уже нужен вывод. Насколько я понимаю, в категориях обычно используется как раз второй вариант, то есть, как отношение эквивалентности с указанными Вами аксиомами.2020 February 06
G
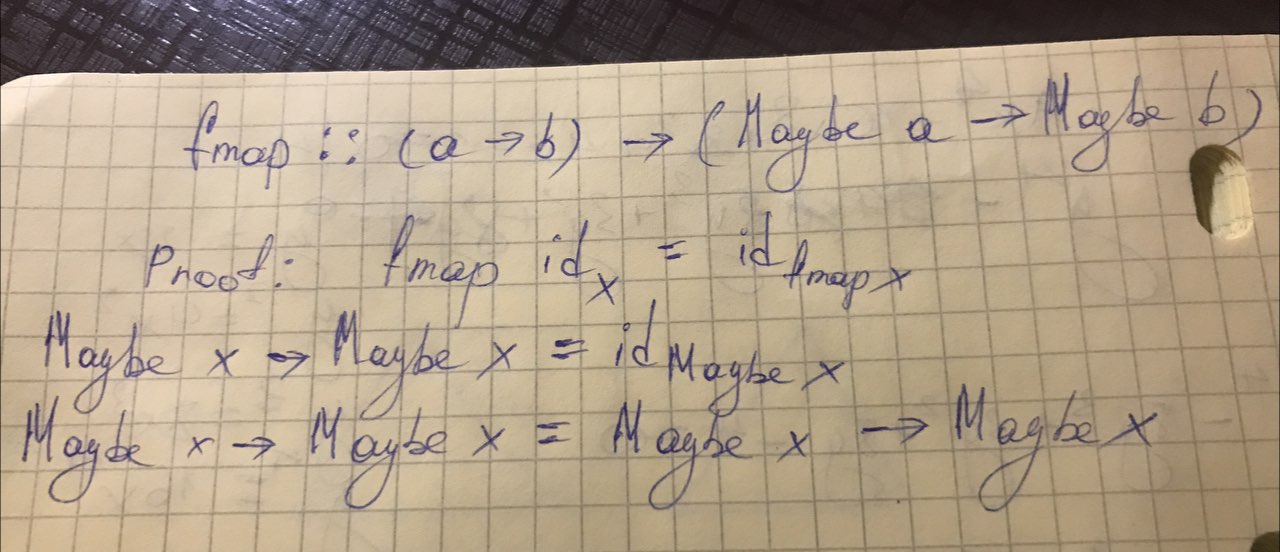
Здравствуйте. В главе про функторы в «Теории категорий для программистов» автор доказывает сохранение идентичного элемента для функтора Maybe. Я решил немного по-другому доказать: не подставлять Just x/Nothing, а сделать так, как показно на картинке. Это верное доказательство?
G
Только что заметил неточность: не
id от fmap x, а id от Maybe x, скорееAZ
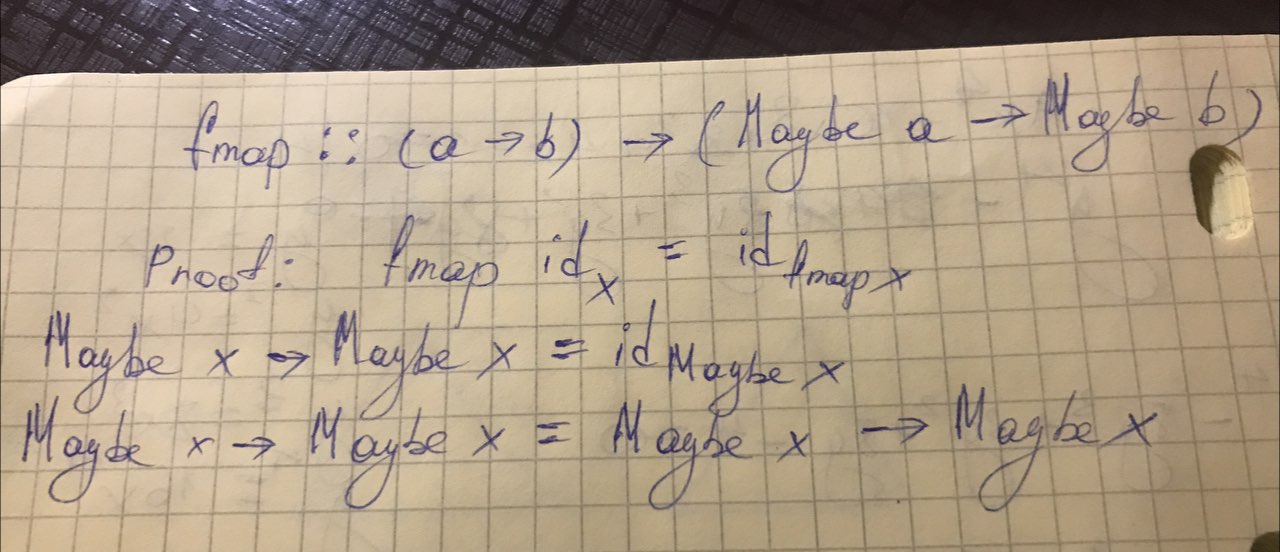
Здравствуйте. В главе про функторы в «Теории категорий для программистов» автор доказывает сохранение идентичного элемента для функтора Maybe. Я решил немного по-другому доказать: не подставлять Just x/Nothing, а сделать так, как показно на картинке. Это верное доказательство?
мне кажется переход от fmap id x к Maybe x -> Maybe x теряет информацию
AZ
потому что
foo = const Nothing тоже Maybe x -> Maybe xOℕ
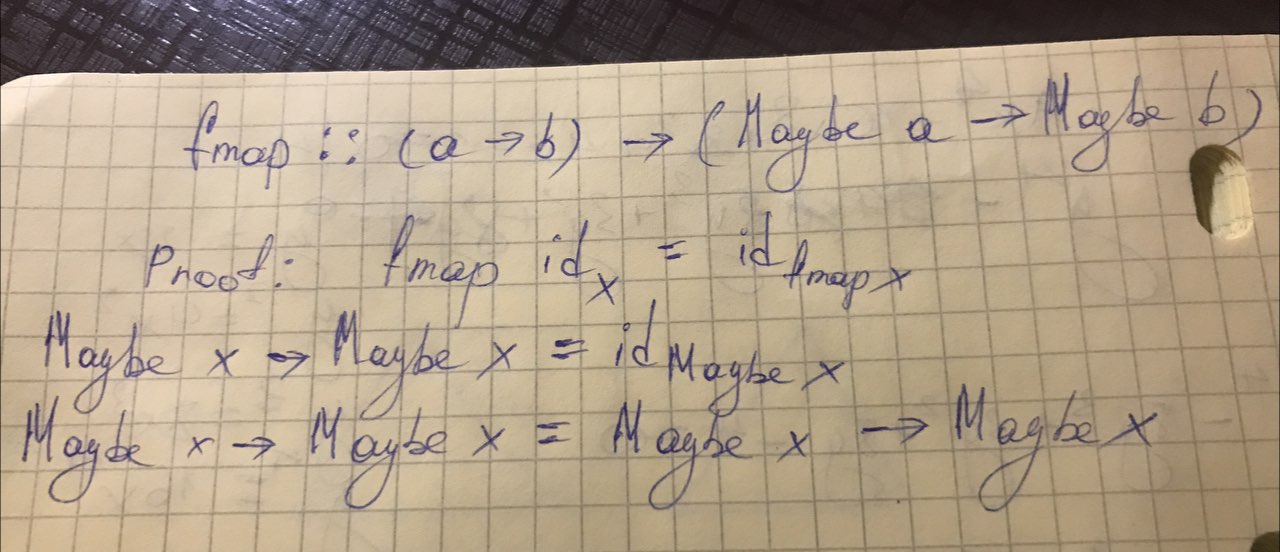
Здравствуйте. В главе про функторы в «Теории категорий для программистов» автор доказывает сохранение идентичного элемента для функтора Maybe. Я решил немного по-другому доказать: не подставлять Just x/Nothing, а сделать так, как показно на картинке. Это верное доказательство?
у Вас в равенстве в третьей строчке типы не сходятся,
слева - тип, а справа - терм
слева - тип, а справа - терм
G
у Вас в равенстве в третьей строчке типы не сходятся,
слева - тип, а справа - терм
слева - тип, а справа - терм
А как правильно?
Oℕ
А как правильно?
С обеих сторон должен быть либо тип, либо термы одного типа
Oℕ
т.е. когда x : A неверно писать х = A
Oℕ
таким образом id @ (Maybe x) имеет тип Maybe x -> Maybe x, но не равен ему
AZ
у Вас в равенстве в третьей строчке типы не сходятся,
слева - тип, а справа - терм
слева - тип, а справа - терм
idris intensifies
G
мне кажется переход от fmap id x к Maybe x -> Maybe x теряет информацию
Теряется информация в том плане, что от id я перехожу к эндоморфизму?
Oℕ
затем вы повторно заменили терм его типом, получив тавтологию
но эта тавтология подразумевается в формулировке
вы лишь получили (неправильным путём), что F (id @ A) и id @ F(A) имеют один тип
но без этого вообще невозможно было бы даже сформулировать утверждение
но эта тавтология подразумевается в формулировке
вы лишь получили (неправильным путём), что F (id @ A) и id @ F(A) имеют один тип
но без этого вообще невозможно было бы даже сформулировать утверждение
G
Так, примерно понял, что не так
TA
Возник вопрос, наверное очень тупой,но все же:
В теории категорий для морфизмов задана конкретная операция композиции.
Но почему никто ещё не отошел от этой концепции и не рассматривал категории как множество объектов и морфизмов для композиции которых в каждой отдельной категории задаются свои правила?
В теории категорий для морфизмов задана конкретная операция композиции.
Но почему никто ещё не отошел от этой концепции и не рассматривал категории как множество объектов и морфизмов для композиции которых в каждой отдельной категории задаются свои правила?
Oℕ
Tel Asc
Возник вопрос, наверное очень тупой,но все же:
В теории категорий для морфизмов задана конкретная операция композиции.
Но почему никто ещё не отошел от этой концепции и не рассматривал категории как множество объектов и морфизмов для композиции которых в каждой отдельной категории задаются свои правила?
В теории категорий для морфизмов задана конкретная операция композиции.
Но почему никто ещё не отошел от этой концепции и не рассматривал категории как множество объектов и морфизмов для композиции которых в каждой отдельной категории задаются свои правила?
В теории категорий в каждой отдельной категории своя собственная операция композиции
Oℕ
Если вас смущают ассоциативность и левая/правая единицы как равенства существует множество обобщений понятия категории
TA
Разве мы не имеем для каждой категории правило:
Hom(B,C) . Hom(A,B)=Hom(A,C)?
Hom(B,C) . Hom(A,B)=Hom(A,C)?
ПД
Tel Asc
Возник вопрос, наверное очень тупой,но все же:
В теории категорий для морфизмов задана конкретная операция композиции.
Но почему никто ещё не отошел от этой концепции и не рассматривал категории как множество объектов и морфизмов для композиции которых в каждой отдельной категории задаются свои правила?
В теории категорий для морфизмов задана конкретная операция композиции.
Но почему никто ещё не отошел от этой концепции и не рассматривал категории как множество объектов и морфизмов для композиции которых в каждой отдельной категории задаются свои правила?
А что содержательного может привнести такое рассмотрение?



