Oℕ
Size: a a a
2020 January 29
А сильная монада является автоматически моноидальным функтором?
AD
Драствуйте, есть ли вменяемое описание того что в коке именуют WellFormed когда просят доказывать терминируемость фикспоинта?
Oℕ
well founded?
Oℕ
А это точно тот чат?
k
В древней книжке TTFP есть тип W, описывающий общий случай индуктивно определённых типов, по идее, все well-founded - его частные случаи. Не в курсе, насколько прямолинейно оно переводится в кок.
KV
kucheryavenkov
В древней книжке TTFP есть тип W, описывающий общий случай индуктивно определённых типов, по идее, все well-founded - его частные случаи. Не в курсе, насколько прямолинейно оно переводится в кок.
В коке есть индуктивные типы
AG
W и расшифровывается как well-founded tree
AG
но это про индуктивные да
2020 January 30
ЮБ
Profunctor optics and traversals
Mario Román
https://arxiv.org/abs/2001.08045
Optics are bidirectional accessors of data structures; they provide a powerful abstraction of many common data transformations.
This abstraction is compositional thanks to a representation in terms of profunctors endowed with an algebraic structure called Tambara module.
There exists a general definition of optic in terms of coends that, after some elementary application of the Yoneda lemma, particularizes in each one of the basic optics.
Traversals used to be the exception; we show an elementary derivation of traversals and discuss some other new derivations for optics.
We relate our characterization of traversals to the previous ones showing that the coalgebras of a comonad that represents and split into shape and contents are traversable functors.
The representation of optics in terms of profunctors has many different proofs in the literature; we discuss two ways of proving it, generalizing both to the case of mixed optics for an arbitrary action.
Categories of optics can be seen as Eilenberg-Moore categories for a monad described by Pastro and Street.
This gives us two different approaches to composition between profunctor optics of different families:
using distributive laws between the monads defining them, and using coproducts of monads.
The second one is the one implicitly used in Haskell programming; but we show that a refinement of the notion of optic is required in order to model it faithfully.
We provide experimental implementations of a library of optics in Haskell and partial Agda formalizations of the profunctor representation theorem.
#paper
Mario Román
https://arxiv.org/abs/2001.08045
Optics are bidirectional accessors of data structures; they provide a powerful abstraction of many common data transformations.
This abstraction is compositional thanks to a representation in terms of profunctors endowed with an algebraic structure called Tambara module.
There exists a general definition of optic in terms of coends that, after some elementary application of the Yoneda lemma, particularizes in each one of the basic optics.
Traversals used to be the exception; we show an elementary derivation of traversals and discuss some other new derivations for optics.
We relate our characterization of traversals to the previous ones showing that the coalgebras of a comonad that represents and split into shape and contents are traversable functors.
The representation of optics in terms of profunctors has many different proofs in the literature; we discuss two ways of proving it, generalizing both to the case of mixed optics for an arbitrary action.
Categories of optics can be seen as Eilenberg-Moore categories for a monad described by Pastro and Street.
This gives us two different approaches to composition between profunctor optics of different families:
using distributive laws between the monads defining them, and using coproducts of monads.
The second one is the one implicitly used in Haskell programming; but we show that a refinement of the notion of optic is required in order to model it faithfully.
We provide experimental implementations of a library of optics in Haskell and partial Agda formalizations of the profunctor representation theorem.
#paper
Кстати, теперь этот же материал есть и в виде поста в n-cafe. С картинками!
https://golem.ph.utexas.edu/category/2020/01/profunctor_optics_the_categori.html
https://golem.ph.utexas.edu/category/2020/01/profunctor_optics_the_categori.html
2020 February 01
G
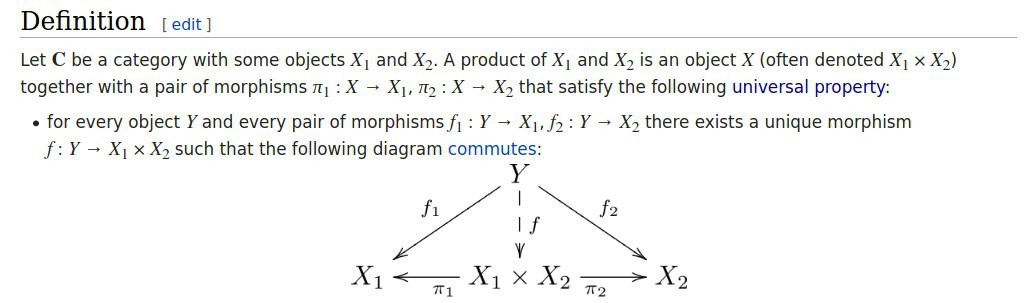
Что здесь означает "... exists a unique morphism f"? Конкретно не понял про unique - уникальный, то есть значит, что всего один?
https://en.wikipedia.org/wiki/Product_(category_theory)
https://en.wikipedia.org/wiki/Product_(category_theory)
Oℕ
Это значит, что любой морфизм, имеющий те же свойства (диаграмма коммутирует), равен этому
Oℕ
Эквивалетно математической нотации ヨ!
Oℕ
Т.е. ты имеешь следующий набор значений
f : Y -> X1 x X2
eq1 : pi1 ∘ f = f1
eq2 : pi2 ∘ f = f2
uniqueness : ∀(g : Y -> X1 x X2) -> (g ∘ pi1 = f1) -> ( g ∘ pi2 = f2) -> g = f
f : Y -> X1 x X2
eq1 : pi1 ∘ f = f1
eq2 : pi2 ∘ f = f2
uniqueness : ∀(g : Y -> X1 x X2) -> (g ∘ pi1 = f1) -> ( g ∘ pi2 = f2) -> g = f
G
Это значит, что любой морфизм, имеющий те же свойства (диаграмма коммутирует), равен этому
Теперь понятно
G
А что значит "Unique up to unique isomorphism"? Это из задания: "Show that the terminal object is unique up to unique isomorphism."
G
Я в Интернете нашёл объяснение, но оно оперирует понятиями, которые я ещё не знаю. Я на пятой главе Теории категорий для программистов (Products and Coproducts)
Oℕ
Уникальность объектов - нетривиальное понятие, выше Ник Иваныч объяснял, что можно ввести гетерогенное равенство.
Но в принципе определение категории не требует наличия какого-то способа идентифицировать объекты.
Поэтому уникальность с точностью до - значит уникальность, где равенство заменено на то, что указано.
Изоморфизм, думаю, понятно что такое. Но изоморфизмов между парой объектов может быть много.
Поэтому уникальный изоморфизм означает, что между объектами гарантировано ровно один изоморфизм
Но в принципе определение категории не требует наличия какого-то способа идентифицировать объекты.
Поэтому уникальность с точностью до - значит уникальность, где равенство заменено на то, что указано.
Изоморфизм, думаю, понятно что такое. Но изоморфизмов между парой объектов может быть много.
Поэтому уникальный изоморфизм означает, что между объектами гарантировано ровно один изоморфизм
Oℕ
Т.е. доказать, что если есть два объекта, удовлетворяющих определению терминального, то между ними есть изоморфизм и он один
G
С заданием стало понятно, спасибо
G
Но немного смущает то, что unique в разных местах означает разное. В первом случае unique морфизм означает, что любой морфизм с такими же свойствами равен ему, а здесь означает, что это ровно один морфизм



