понятно

Perhaps you think it is OK to pretend that something is a category when it is not. In that case, you would also pretend that the Haskell monads are actual category-theoretic monads. I recall a story from one of my math professors: when she was still a doctoral student she participated as “math support” in the construction of a small experimental nuclear reactor in Slovenia. One of the physicsts asked her to estimate the value of the harmonic series  1 + 1/2 + 1/3 + ⋯  to four decimals. When she tried to explain the series diverged, he said “that’s ok, let’s just pretend it converges”.
:)

А катаморфизм это всегда какой-то фолд?

Нет, не всегда. Зависит от категории и функторов.
Если они достаточно "хорошие", то будет похоже на fold.
А так, можно представить какие-нибудь категории, совсем не похожие на "программистские", ну и функторы соответственно.

Никак не могу понять смысл... Попробую заглянуть дальше, мб будет какая-то интуиция. Да, там дальше эта категория используется для определения универсальной стрелки

Ну это не строго обязательное.
Хотя и иногда, бывает удобно.
Те же универсальные стрелки несложно определяются непосредственно.

Ощущение, что это  очень мутное описание унрверсальной стрелки и есть. Даже диаграмма точно такая же

А можете меня кто-нибудь ткнуть в непосредственное определение универсальной стрелки? (книга/стр). Универсальная значит: начальная либо терминальная?

Посмотри другое определение категории запятой, это несложный  концепт на самом деле

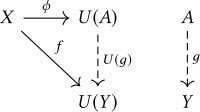
Если правильно помню,  мы берем функтор U и подсвечиваем кусочек C подобный D. Фиксируем объект A из C. Строим категорию запятой:
1. Объектами будут стрелки из A в образ D
2. Если между стрелкой A-> х и A->y (x,y из образа)  есть стрелка x->y, то добавляем стрелку между соответствующими объектами  в категорию запятой

Непосредственно — это без рассмотрения дополнительных категорий, видимо. Можно определить универсальную стрелку как инициальную/терминальную в какой-то вспомогательной категории, а можно без этого, просто заинлайнив некоторые детали

Спасибо, да, как раз читаю... Всем спасибо за ответы!

А вообще. Я тут кидал учебник для физиков. Там хорошо написано и об этом. С красивыми примерами

Interaction laws of monads and comonads
Shin-ya Katsumata, Exequiel Rivas, Tarmo Uustalu
https://arxiv.org/abs/1912.13477
We introduce and study functor-functor and monad-comonad interaction laws as mathematical objects to describe interaction of effectful computations with behaviors of effect-performing machines.
Monad-comonad interaction laws are monoid objects of the monoidal category of functor-functor interaction laws.
We show that, for suitable generalizations of the concepts of dual and Sweedler dual, the greatest functor resp. monad interacting with a given functor or comonad is its dual while the greatest comonad interacting with a given monad is its Sweedler dual.
We relate monad-comonad interaction laws to stateful runners.
We show that functor-functor interaction laws are Chu spaces over the category of endofunctors taken with the Day convolution monoidal structure.
Hasegawa's glueing endows the category of these Chu spaces with a monoidal structure whose monoid objects are monad-comonad interaction laws.
#paper

During the 20th century, mathematical logic
was found to be inadequate, and the current state of mathematical logic is still far from satisfactory, bogged down in convoluted, mutually incompatible frameworks which have dubious relevance to the real-world mathematics issues which they were originally intended to resolve. The fact that practical mathematics has
continued in blissful disregard of the paradoxes and the plethora of formalisms in the last 120 years gives
some indication of the irrelevance of most mathematical logic research to most practical mathematics

Спасибо

Seems like math/logic related statements should be more strict than this emotional sentence with unclear arguments

Так, это не про теоркат