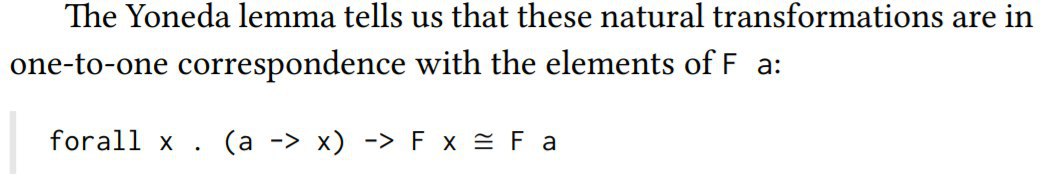ЕО
Size: a a a
2019 December 23
Я скоро вам запрещу нетотальные языки обсуждать вообще :)
Oℕ
По койонеде и экзистенциальным типам вам объяснили, должно было стать понятно, что исходное ваше выражение не выражает коЙонеду
AZ
По койонеде и экзистенциальным типам вам объяснили, должно было стать понятно, что исходное ваше выражение не выражает коЙонеду
нет, не понятно. То что там написано очень похоже на ваш
exists a. (a -> x, f a) <~> f x. А код который я скинул как раз требует Rank-N types, то есть логично предположить, что он как раз и нужен для экзистенциалов. И как раз эту идею и выражает.Oℕ
предлагаю тогда в тишине помедитировать над статьями, над хаскельным типом койонеды
AZ
Oℕ
и уточнить в другой группе, какие кванторы расставляет haskell неявно
МБ
Все беды Haskell от того, что они никак не могут договориться о стандартных расширениях.
Oℕ
нет, не понятно. То что там написано очень похоже на ваш
exists a. (a -> x, f a) <~> f x. А код который я скинул как раз требует Rank-N types, то есть логично предположить, что он как раз и нужен для экзистенциалов. И как раз эту идею и выражает.МБ
Все беды Haskell от того, что они никак не могут договориться о стандартных расширениях.
Можно все примеры на Clean переписать. Будет хотя бы однозначно. Думаете, имеет смысл использовать Clean в учебном пособии?
NI
;-)
idris-ct: A Library to do Category Theory in Idris
Fabrizio Genovese, Alex Gryzlov, Jelle Herold, Andre Knispel, Marco Perone, Erik Post, André Videla
https://arxiv.org/abs/1912.06191
We introduce idris-ct, a Idris library providing verified type definitions of categorical concepts.
idris-ct strives to be a bridge between academy and industry, catering both to category theorists who want to implement and try their ideas in a practical environment and to businesses and engineers who care about formalization with category theory:
It is inspired by similar libraries developed for theorem proving but remains very practical, being aimed at software production in business.
Nevertheless, the use of dependent types allows for a formally correct implementation of categorical concepts, so that guarantees can be made on software properties.
#paper
idris-ct: A Library to do Category Theory in Idris
Fabrizio Genovese, Alex Gryzlov, Jelle Herold, Andre Knispel, Marco Perone, Erik Post, André Videla
https://arxiv.org/abs/1912.06191
We introduce idris-ct, a Idris library providing verified type definitions of categorical concepts.
idris-ct strives to be a bridge between academy and industry, catering both to category theorists who want to implement and try their ideas in a practical environment and to businesses and engineers who care about formalization with category theory:
It is inspired by similar libraries developed for theorem proving but remains very practical, being aimed at software production in business.
Nevertheless, the use of dependent types allows for a formally correct implementation of categorical concepts, so that guarantees can be made on software properties.
#paper
ЕО
Я за то, чтобы туториалы на агде писать
МБ
А какая от этого выгода?
МБ
;-)
idris-ct: A Library to do Category Theory in Idris
Fabrizio Genovese, Alex Gryzlov, Jelle Herold, Andre Knispel, Marco Perone, Erik Post, André Videla
https://arxiv.org/abs/1912.06191
We introduce idris-ct, a Idris library providing verified type definitions of categorical concepts.
idris-ct strives to be a bridge between academy and industry, catering both to category theorists who want to implement and try their ideas in a practical environment and to businesses and engineers who care about formalization with category theory:
It is inspired by similar libraries developed for theorem proving but remains very practical, being aimed at software production in business.
Nevertheless, the use of dependent types allows for a formally correct implementation of categorical concepts, so that guarantees can be made on software properties.
#paper
idris-ct: A Library to do Category Theory in Idris
Fabrizio Genovese, Alex Gryzlov, Jelle Herold, Andre Knispel, Marco Perone, Erik Post, André Videla
https://arxiv.org/abs/1912.06191
We introduce idris-ct, a Idris library providing verified type definitions of categorical concepts.
idris-ct strives to be a bridge between academy and industry, catering both to category theorists who want to implement and try their ideas in a practical environment and to businesses and engineers who care about formalization with category theory:
It is inspired by similar libraries developed for theorem proving but remains very practical, being aimed at software production in business.
Nevertheless, the use of dependent types allows for a formally correct implementation of categorical concepts, so that guarantees can be made on software properties.
#paper
Странно. Но ладно. А где исходники можно посмотреть?
AZ
ну или
exists a (x -> a, f a) <~> f a
для контравариантных
exists a (x -> a, f a) <~> f a
для контравариантных
а откуда ты exists взял?
ЗП
тут сказано про лемму Йонеды, но есть еще и Койонеда
концы vs коконцы
концы vs коконцы
AZ
phi :: forall a f . (forall x . (a -> x) -> f x) -> f a
phi alpha = alpha id
psi :: forall a f . Functor f => f a -> (forall x . (a -> x) -> f x)
psi fa h = fmap h faAZ
вот ведь, нет?