Вот такая задача с семинара учителей сейчас, например:

Пусть CH — высота прямоугольного треугольника ABC. Докажите, что CH — сумма радиусов вписанных окружностей треугольников ABC, ACH, BCH.

Geometriyadan ajoyib savollar.

https://t.me/MathRmm

Равносторонний треугольник APQ вписан в прямоугольник ABCD как показано на рисунке. M — середина AP. Докажите, что треугольник CDM тоже правильный.

коллега Кноп поделился в комментариях обобщением предыдущего:

если правильный треугольник APQ вписан в параллелограмм ABCD, то вершина M правильного треугольника CDM все равно лежит на AP (хотя уже не обязательно является серединой отрезка)

Школа Skysmart (часть Skyeng) объявляет набор преподавателей по математике. Нужны учителя с опытом работы от 1 года.

Условия:

🔺 График онлайн-занятий, который можно подстроить под себя;
🔺 Готовые учебные материалы и автопроверка д/з;
🔺 Кураторская поддержка по любому вопросу.

Как принять участие в отборе?

1) Зайти на сайт Skyeng по ссылке;
2) Выбрать «Математика»;
3) Ввести свои контакты в специальной форме и нажать на кнопку «Оставить заявку».

Дальше будет заполнение анкеты, вводное обучение и пробный урок.

Поделитесь с теми, кому это может быть интересно 👀

#реклама

задача из статьи Л.Емельянова в свежем Кванте: рассмотрим окружность и касательную к ней; по этой касательной скользит красный отрезок AB фиксированной длины — найти ГМТ зеленых точек пересечения касательных к окружности из точек A и B

динамический чертеж: https://www.geogebra.org/m/hpepuzw2

журнал «Квант»: http://kvant.mccme.ru/ (в №11-12 за 2021 год есть спойлеры)

Глеб Минаев написал¹ свое решение задачи из предыдущего поста… и по пути предлагает рассмотреть вместо окружности параболу

динамический чертеж: https://www.geogebra.org/m/kuqhhfak

¹ https://t.me/c/1280979137/1738

Оказывается, верно такое обобщение известного признака равногранного тетраэдра (via В.В.Прасолов, который прочитал это в препринте arXiv:2112.14918).

Если у тетраэдра две пары равновеликих граней, то в каждой паре грани буквально равны.

Семинар МЦНМО

Сегодня 3 февраля в 19:00 в МЦНМО (Бол.Власьевский, 11).

Д.В.Прокопенко
Доклад будет состоять из двух частей.

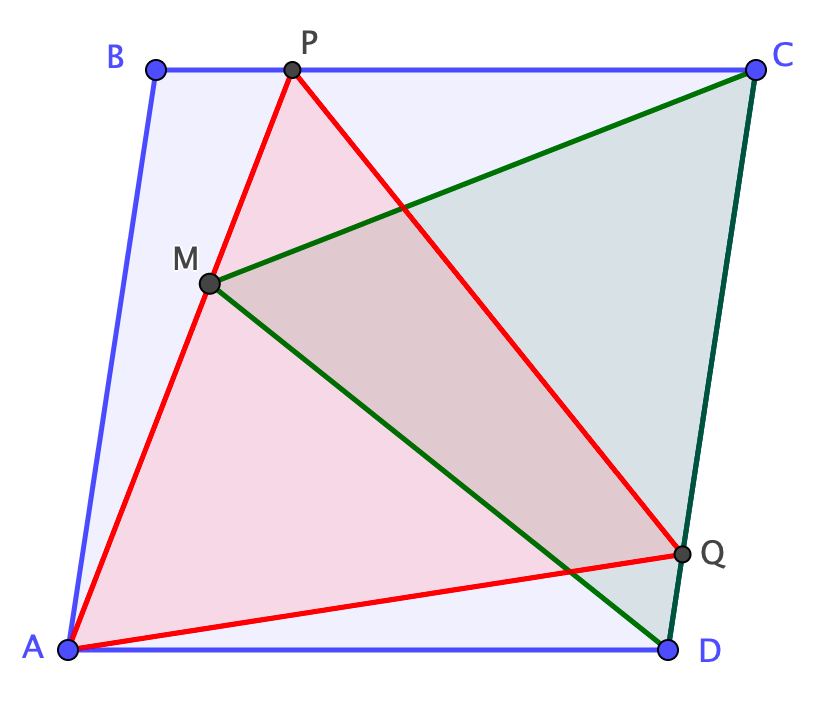
В первой мы будем рассматривать задачи, в которых используем две теоремы:
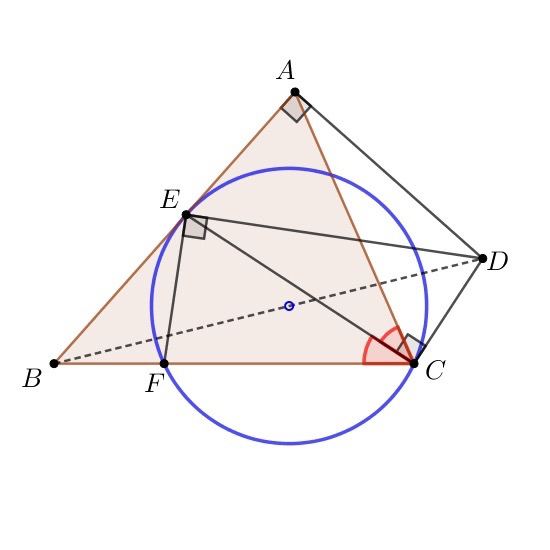
1) проекции вершины на биссектрисы треугольника лежат на средней линии
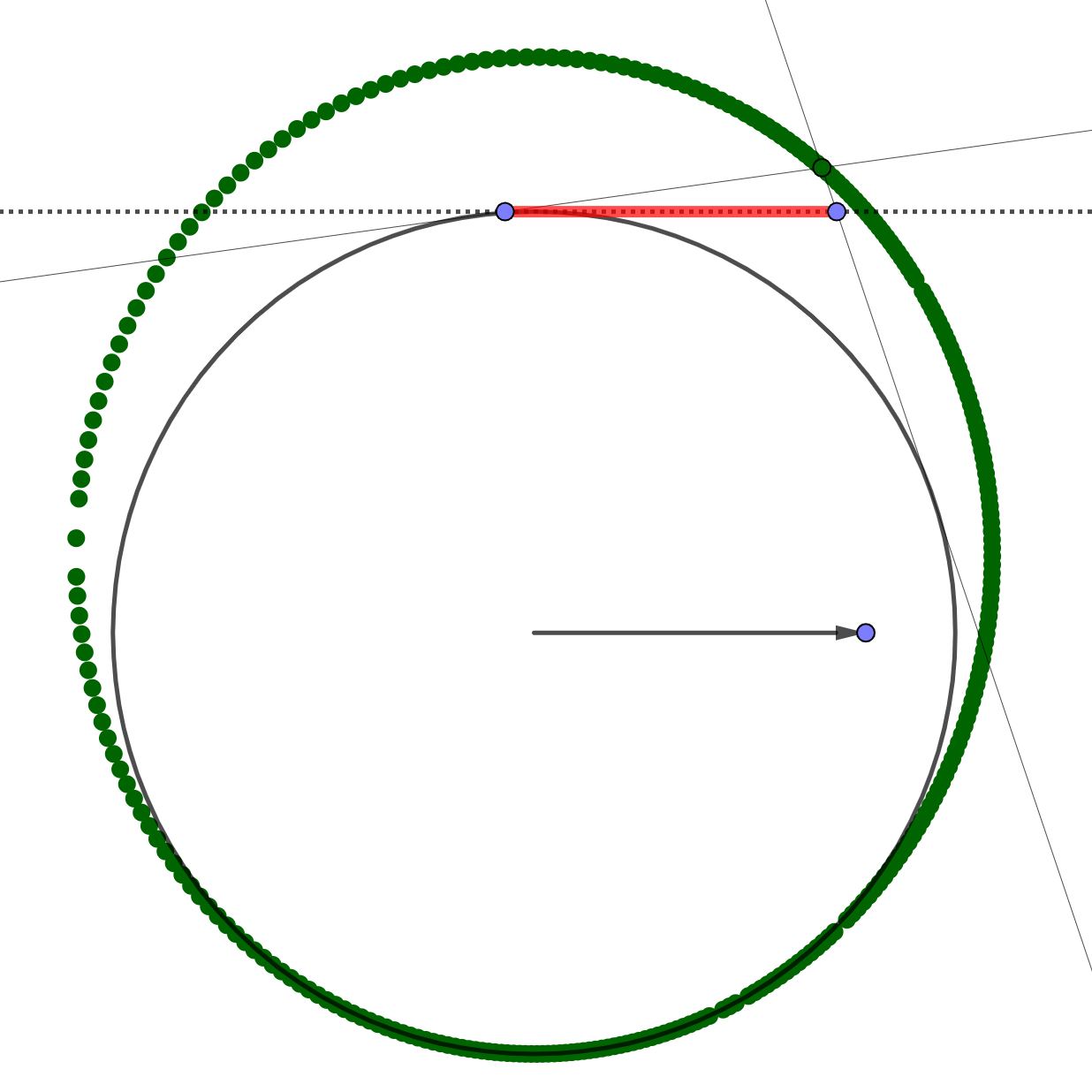
2) прямую Симсона как признак того, что точка лежит на окружности.
Потом совместим эти две теоремы и будем доказывать, что четыре точки лежат на одной окружности.

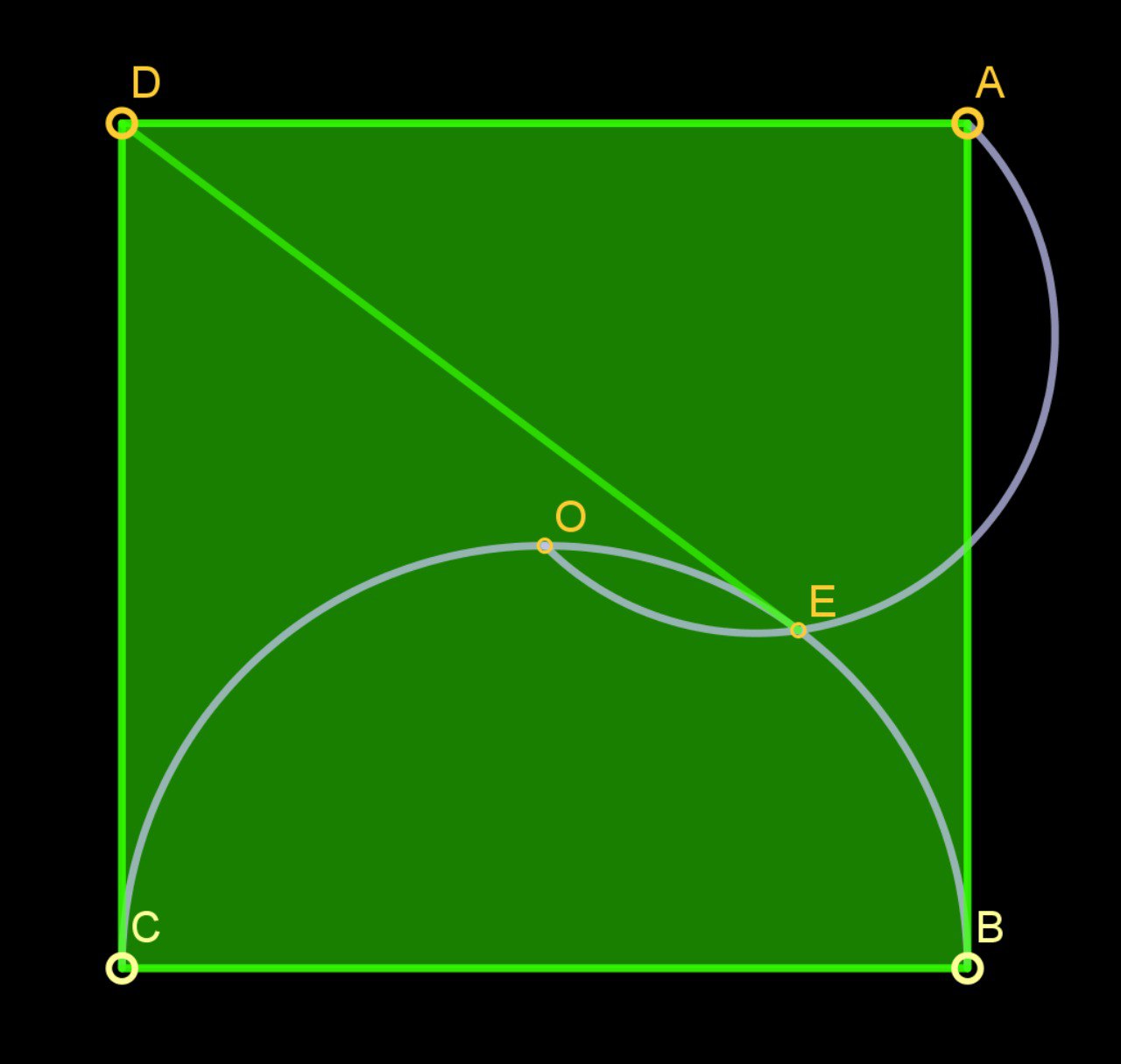
Неожиданно в разных задачах возникает «средняя линия треугольника как прямая Симсона». При этом возникают симпатичные конструкции. Мы попробуем найти общее в таких разных, на первый взгляд, задачах.

Во второй части окажется, что на самом деле все это нужно, чтобы ответить на вопрос где лежит ортоцентр. Оказывается, что, решая задачи из первой части, мы уже можем ответить на этот вопрос.

Сайт семинара: https://mccme.ru/nir/seminar/

И признак равногранного тетраэдра, и его обобщение выше совсем легко следует из теоремы Минковского о ежах.

Про теорему Минковского и ее следствия можно послушать лекцию В.Ю.Протасова на ЛШСМ-2019 (рассуждение про тетраэдры примерно через 30 минут от начала).

Видео: http://www.mathnet.ru/present24980

Всероссийская олимпиада 2022, региональный этап, первый день, задача 9.5.

Пусть CE — биссектриса в остроугольном треугольнике ABC. На внешней биссектрисе угла ACB отмечена точка D, а на стороне BC — точка F, причем ∠BAD=90°=∠DEF. Докажите, что центр окружности, описанной около треугольника CEF, лежит на прямой BD.

O - центр квадрата ABCD. Полуокружности, построенные на диаметрах BС и AO, пересекаются в точке E (отличной от O). Докажите наглядно *), что длина DE равна стороне квадрата.

*) слово "наглядно" означает, что решение в духе "напишем уравнения окружностей, найдем координаты E и вычислим расстояние DE по теореме Пифагора" - это не то, что хочется увидеть автору задачи.

Забавное утверждение, которого я почему-то до сегодняшнего дня не знал. Если есть две параболы с параллельными осями симметрии, то их общая хорда делит отрезок общей касательной пополам.

Среди всяких теорем о касающихся окружностях есть, конечно, не мало удивительных. Но вот, так называемая, теорема о семи окружностях это сравнительно недавнее изобретение. Этот факт был обнаружен только в 1974-м году тремя авторами (Evelyn, Money-Coutts, and Tyrrell). Утверждение состоит в следующем.

Шесть окружностей (синих) составляют окружностей, касающихся друг друга по цепочке и касающихся данной красной окружности. Тогда диагонали шестиугольника с вершинами в точках касания пересекаются в одной точке.

перевод фрагмента книги «Теорема о семи окружностях и другие новые теоремы» Ивлина, Мани-Каутса и Тиррелла (в т.ч. доказательство теоремы о семи окружностях) напечатан в выпуске 23 «Математического просвещения»
http://mi.mathnet.ru/mp927

а в выпуске 25 есть другое доказательство теоремы о семи окружностях от Глеба Минаева
http://mi.mathnet.ru/mp965

появилась видеозапись рассказа Димы Швецова про вписанную окружность (семинар учителей математики 20.01.2022, МЦНМО):

https://youtu.be/OngSmVd60t4
https://mccme.ru/nir/seminar/

Привет! На связи бот Поли 🤖
⠀
Я помогу тебе подготовиться к ЕГЭ, определиться с вузом и не пропустить важные даты!

Специально для тех, кто еще не определился с профессией, у меня есть профориентационный тест, советую начать с него 📲
⠀
Обещаю присылать только полезную информацию и не спамить 👋

Подпишись, бот Поли — лучший друг и помощник абитуриента.

#реклама

https://www.iucr.org/news/newsletter/volume-27/number-3/deformed-penrose-tiling-and-quasicrystals

картинки по выходным: мозаика Пенроуза и ее деформации

Онлайн-ярмарка образовательных товаров и услуг

Приглашаем участвовать в онлайн-ярмарке образовательных товаров и услуг в канале matolimp. Аудитория канала и групп matolimp — родители школьников из Москвы, интересующиеся олимпиадами и поступлением в топовые школы.

Расскажите на Ярмарке о кружках для школьников, индивидуальных и групповых занятиях, весенних и летних лагерях, офлайн и онлайн интенсивах, об образовательных онлайн-сервисах и платформах, об экскурсиях — обо всём, что может быть интересно родителям мотивированных школьников из Москвы.

Ярмарка пройдёт с 4 по 10 марта. Госшколы, компании с госденьгами и специальные гости могут размещаться бесплатно, для остальных стоимость участия от 3000 рублей в зависимости от типа услуги и параметров объявления. При самом раннем (до 18 февраля) и раннем (до 25 февраля) бронировании действуют скидки до 15%..

Участвуйте сами и расскажите другим руководителям образовательных проектов о ярмарке в канале @matolimp
Условия участия, отзывы участников прошлых ярмарок и более подробную информацию можно получить у @maxim_dmitriev
#реклама