к вопросу из чата о том, есть ли что-либо интересное в задачах в этом канале — вот еще продолжение этого сюжета от коллеги Клепцына: https://t.me/mathtabletalks/4030 и далее в том канале

Если вы разделите полный угол на n равных углов, поместите одинаковые ромбы в каждый из уголов, а затем продолжите заполнять ромбами внешность получившейся звезды, то при нечетном n после (n-1)/2 шагов получится правильный 2n-угольник. Если n четное, то после (n-2)/2 шагов получится правильный n-угольник. На рисунке n = 19. А по ссылке можно поподставлять разные n: https://paolini.github.io/rosette/

https://twitter.com/panlepan/status/1472218266420588548

эта #задача здесь уже была под номером 32 — а вот к ней красивые картинки

А.И.Сгибнев поделился:

Статья про механизмы для вычерчивания конических сечений. Иллюстрации из книги Франса ван Схотена (1615-1660), голландского математика, публикатора Декарта и Виета, учителя Гюйгенса. А также динамические чертежи в Геогебре. Параболограф и четыре разных эллипсографа. Можно сделать неплохой проект со школьниками.

https://www.maa.org/press/periodicals/convergence/historical-activities-for-calculus-module-1-curve-drawing-then-and-now

Американский классик Геогебры Стив Фелпс предложил симпатичный набор задачек на восстановление треугольника по данным элементам — комбинациям вершин, высот и ортоцентра. Новизна в том, что треугольники этими данными определяются неоднозначно, остаются степени свободы и надо построить "самый гибкий возможный треугольник", т.е. семейство. Неплохое упражнение для 7 класса. Мб, такие задания школьники легче воспримут, чем "построй ГМТ вершин".

https://www.geogebra.org/m/xrwmzyf7#

(В задании 2 вроде нет решения — не знаю, фича это или бага.)

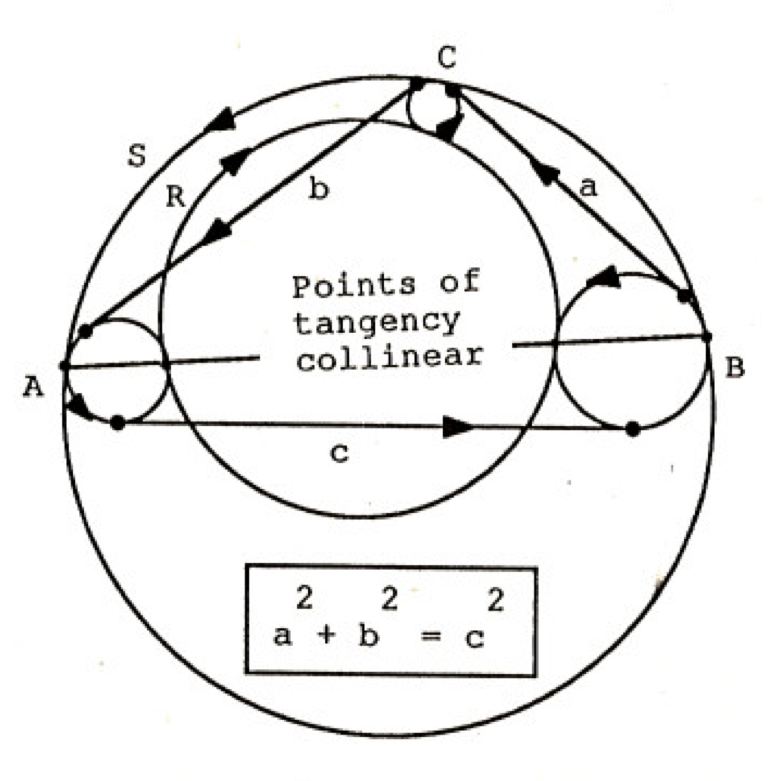
в качестве первой задачи нового года — теорема Пифагора…

…ну то есть почти: все точки в теореме Пифагора заменили на окружности (а расстояния между точками — на длины общих касательных)

кроме решения — интересны другие примеры таких родственников классических теорем

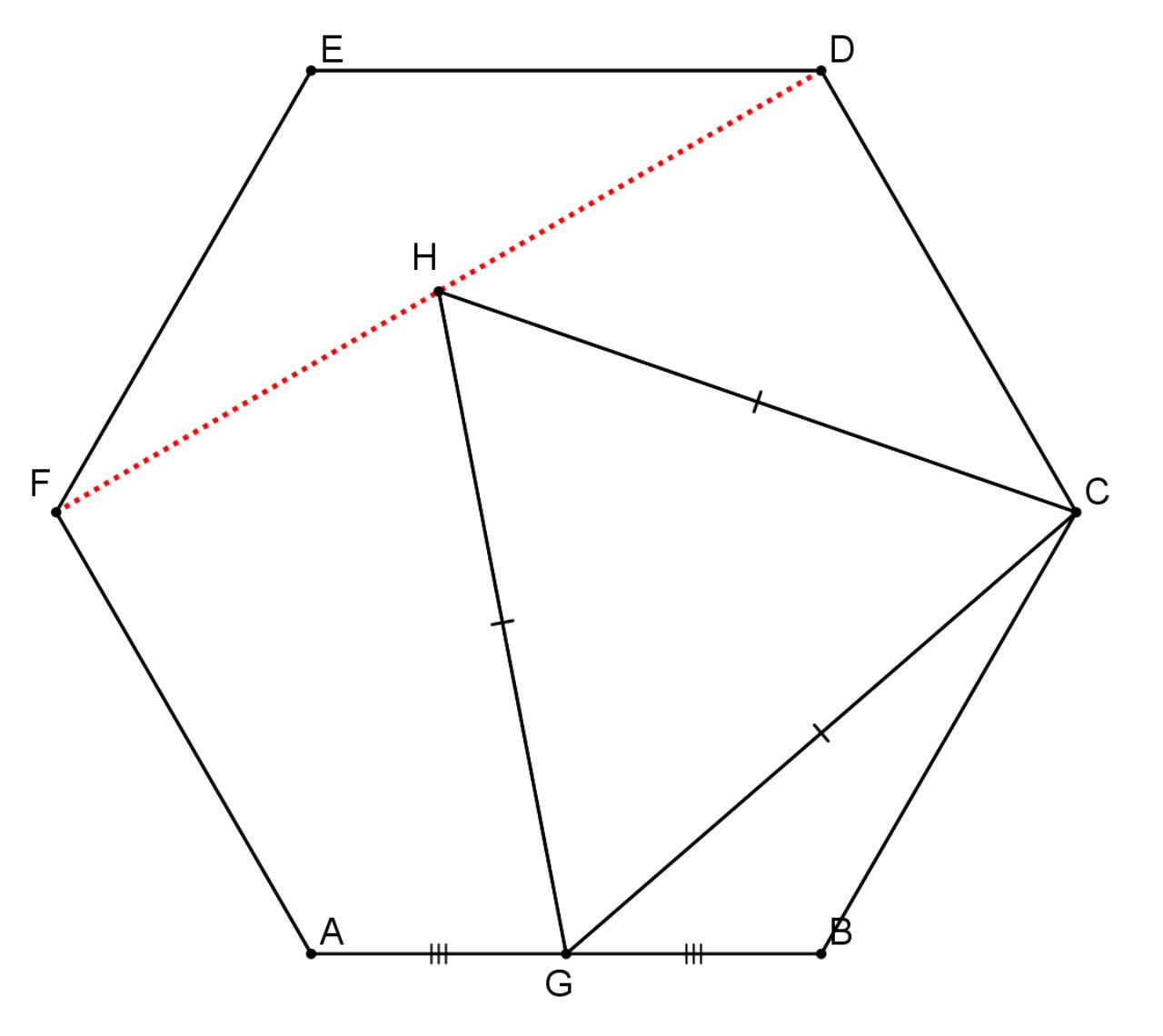
Придумайте как можно более "детское" решение такой вот задачи:


G - середина стороны AB правильного шестиугольника ABCDEF, правильный треугольник GCH лежит внутри шестиугольника. Доказать, что H - середина отрезка DF.

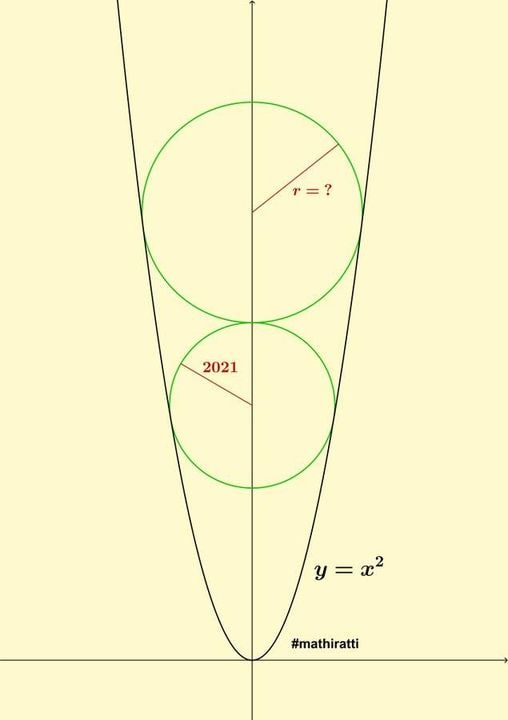
Забавная геометрическая задачка от математика Диего Раттажжи.

Мне тут напомнили, что сегодня каналу ровно 5 лет. Спасибо всем, кто был с самого начала, и всем, кто присоединился позже.

выше — задачи иранской геометрической олимпиады этой осени (via https://math.mosolymp.ru/olympiads_igo_2021 — там еще есть результаты и статистика по России)

Если вы в Москве, приходите 20 января послушать Дмитрия Швецова про вписанную окружность:

Семинар МЦНМО

Начало: 19:00 (Рекомендуем прийти пораньше и заглянуть в магазин «Математическая книга».)
Адрес: Большой Власьевский переулок, дом 11.
Регистрация не нужна.

Д.В.Швецов «Вписанная окружность»
Н.А.Наконечный «Кружок по математике в начальной школе»

Сайт семинара: https://mccme.ru/nir/seminar/

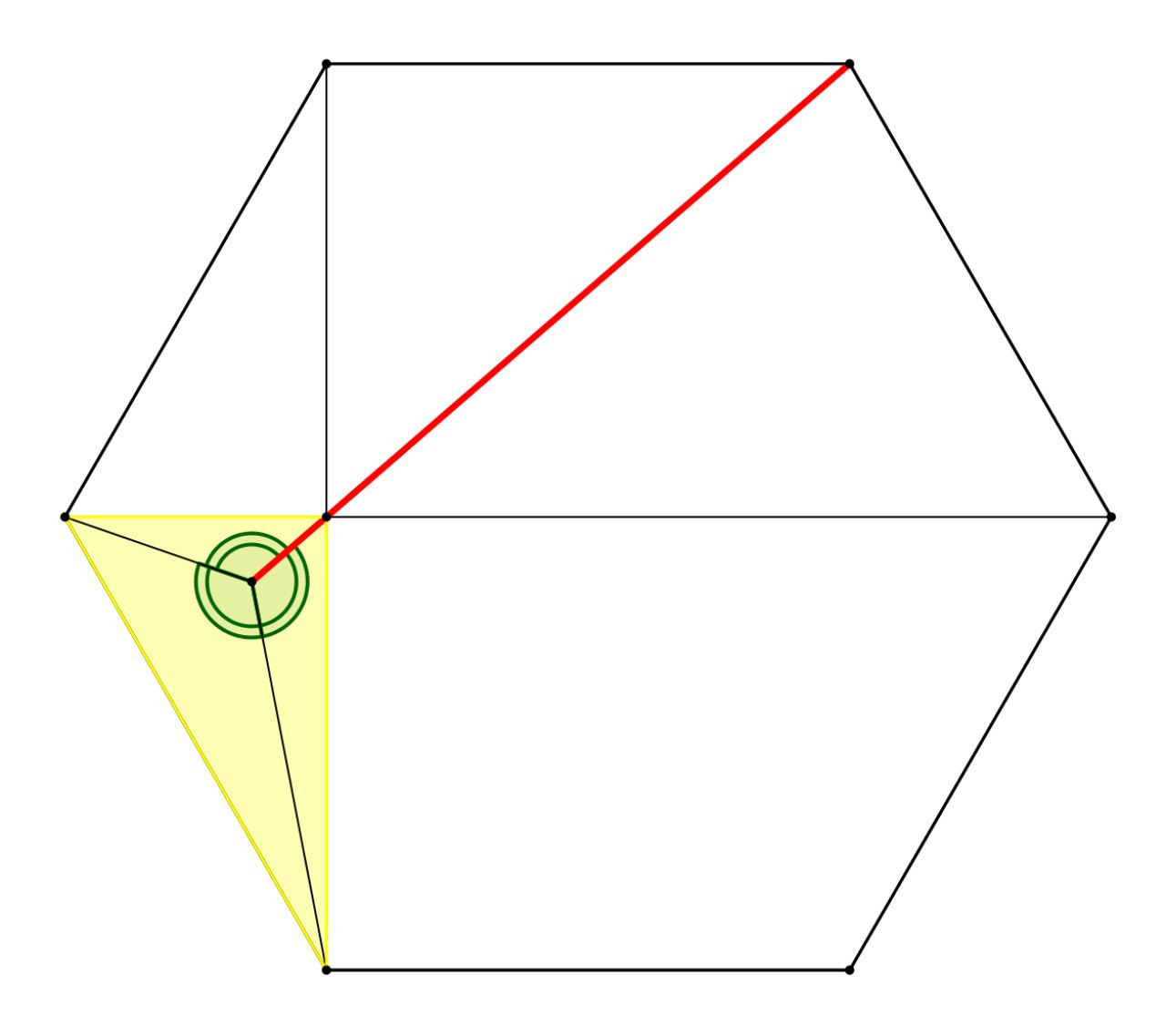
Докажите, что точка Торричелли желтого прямоугольного треугольника, вершина его прямого угла и одна из вершин правильного шестиугольника - коллинеарны.

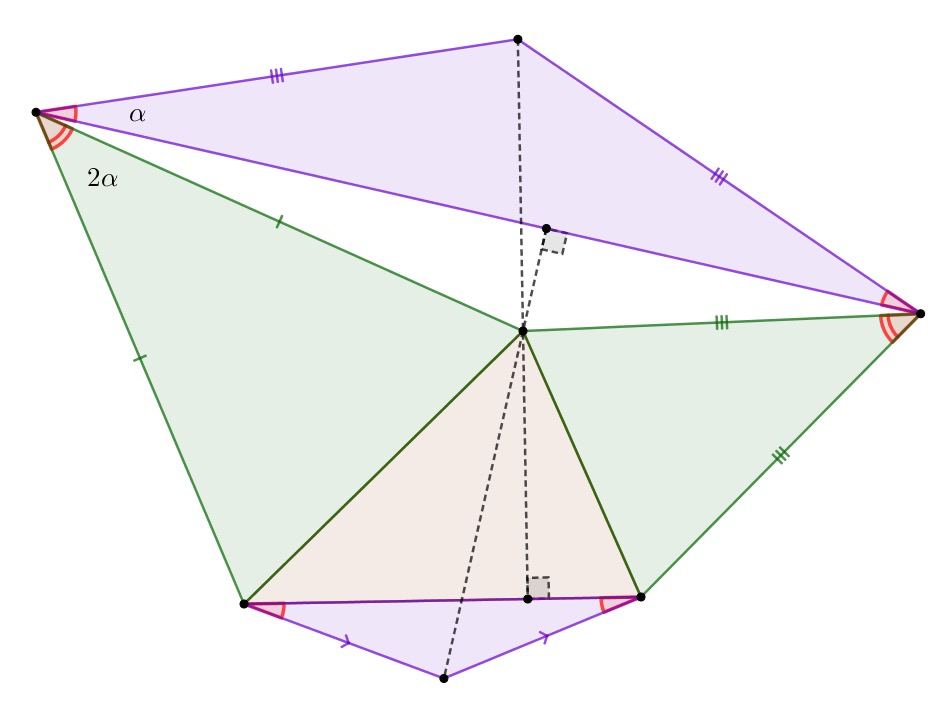
В группе Romantics of Geometry (https://www.facebook.com/groups/parmenides52/) встретился с одним очень симпатичным утверждением, которого раньше не знал. Автор Floor van Lamoen.

Все необходимое есть на картинке. Требуется доказать две перпендикулярности.

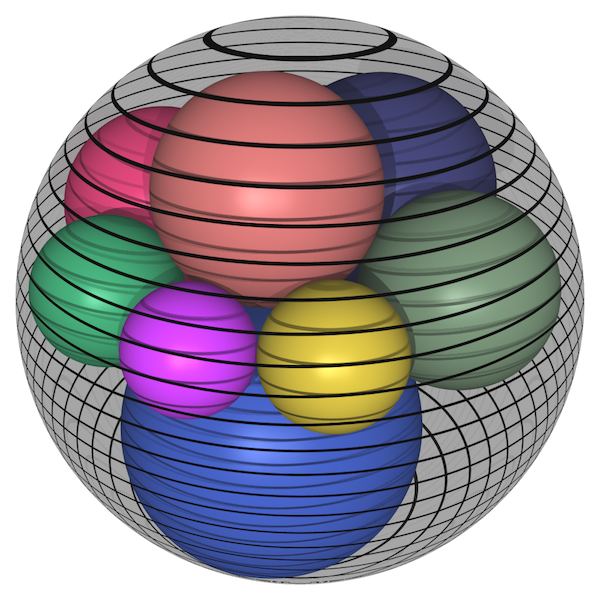
сегодняшняя картинка — гекслет Содди¹:

зафиксируем три попарно касаюшиеся сферы (две меньших внутри большей) и начнем строить цепочку шаров, каждый из которых касается трех фиксированных сфер и предыдущего шара цепочки

тогда эта цепочка непременно замкнется после 6-го шага

===

¹ Фредерик Содди — английский радиохимик, лауреат Нобелевской премии

теорема выглядит (по-моему) удивительно — ср., например, с поризмом Штейнера (где и цепочка не всегда замыкается, и если замыкается — может быть сколько угодно шагов)

но доказать ее совсем не сложно: сделаем инверсию с центром в точке касания двух фиксированных сфер — они превратятся в две параллельные плоскости, а третья фиксированная сфера — в зажатый между ними шар

ну тут уж понятно, что в цепочке будет ровно 6 шаров

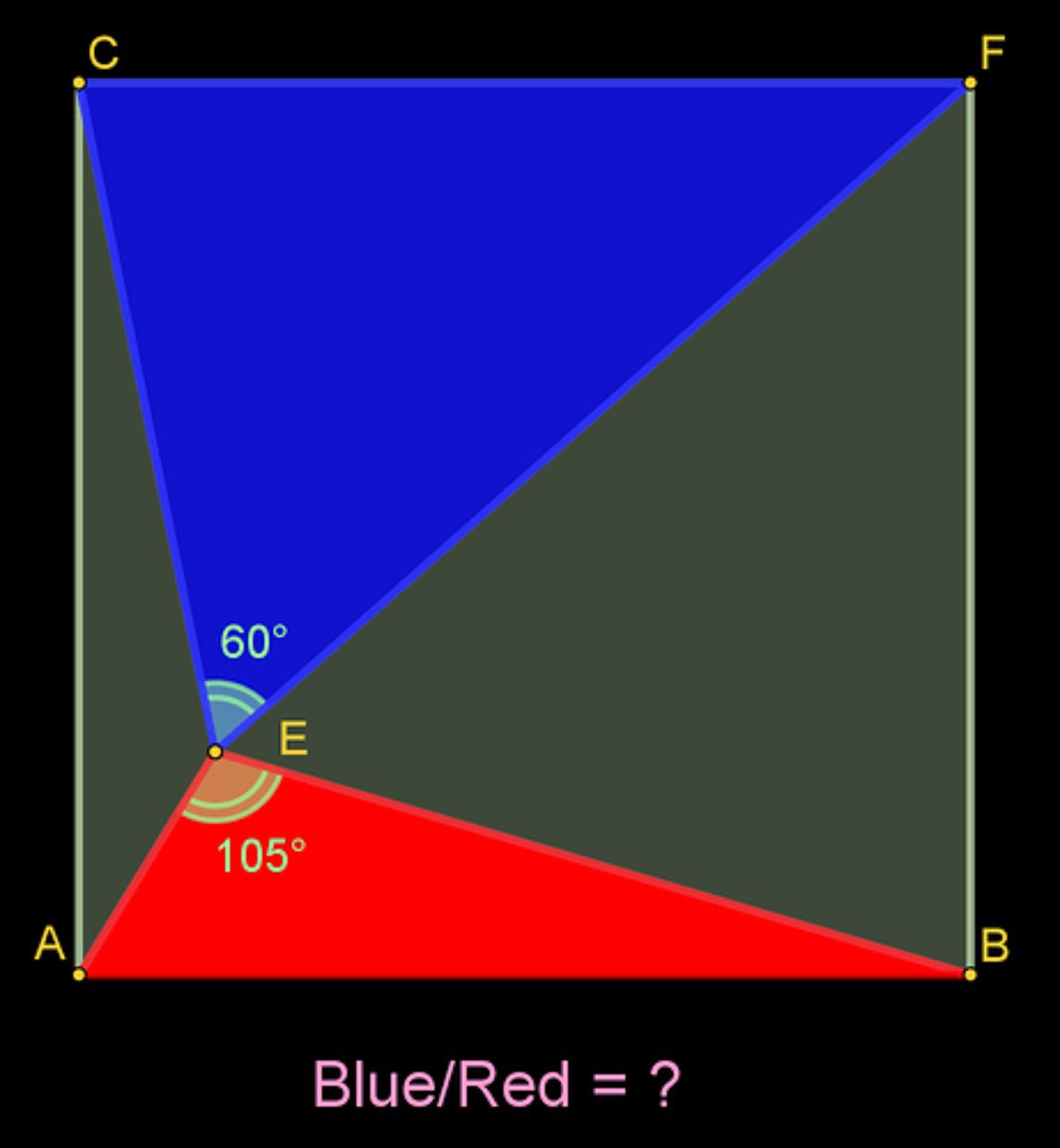
Кто хочет попробовать свои силы без тригонометрии и пр.?