Новое видео с Александром Владимировичем о вписанных углах:

https://youtu.be/MKv6vzzSdZk

Всем привет!
Вчера прошла районная олимпиада по математике Санкт-Петербурга, она же по совместительству является муниципальным этапом Всероссийской в Санкт-Петербурге. Предлагаю посмотреть на геометрические задачи этой олимпиады.

7. 3. На стороне AB треугольника ABC выбрана точка D, а на стороне BC — точка E. Точка F отмечена так, что отрезки EF и BD пересека- ются. Оказалось, что AB = BC, BD = CD = CE = EF, AC = BF. Докажите, что точки C, D, F лежат на одной прямой.

#задача доказать, что синий четырехугольник описанный

https://www.geogebra.org/m/utqyjjjq

https://youtu.be/PH7IDlYD7f8

«Неужели все красивые факты геометрии были найдены в Древней Греции, и нам лишь остается изучать их доказательства? Вовсе нет! Давайте вспомним теоремы Морли, Тебо, Помпею, а также окружности Конвея и Ламуна»

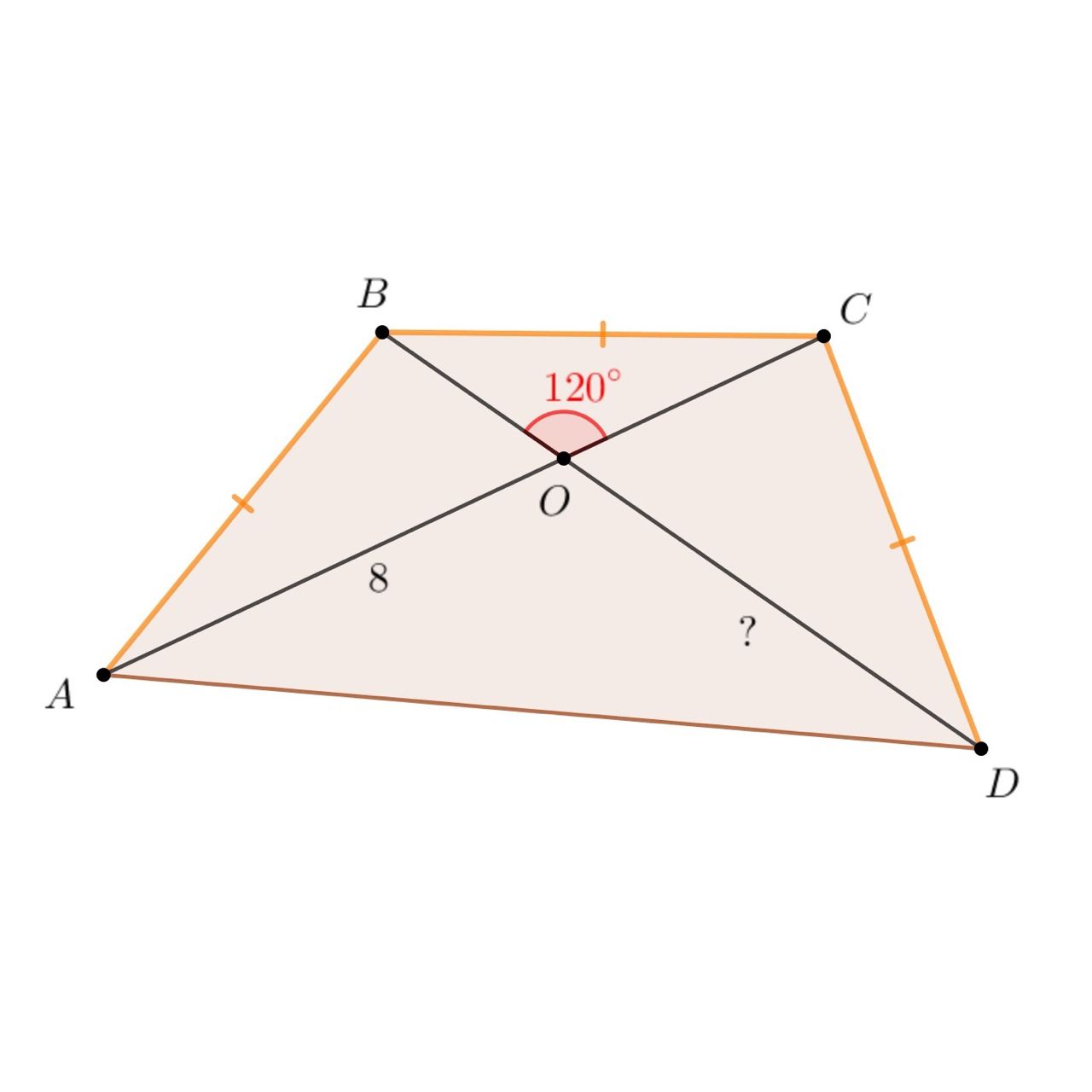
Всем привет! А вот и геометрические задачи муниципального этапа ВсОШ в Татарстане.

8.5. Диагонали четырехугольника ABCD пересекаются в точке O. Известно, что AB = BC = CD, AO = 8 и ∠BOC = 120° . Чему равно DO?

два новых ролика А.Щетникова про сангаку

https://youtu.be/wr9xlp96rSs
https://youtu.be/uJBAibgzf_g

К этому ролику хочется добавить маленькое геометрическое продолжение.

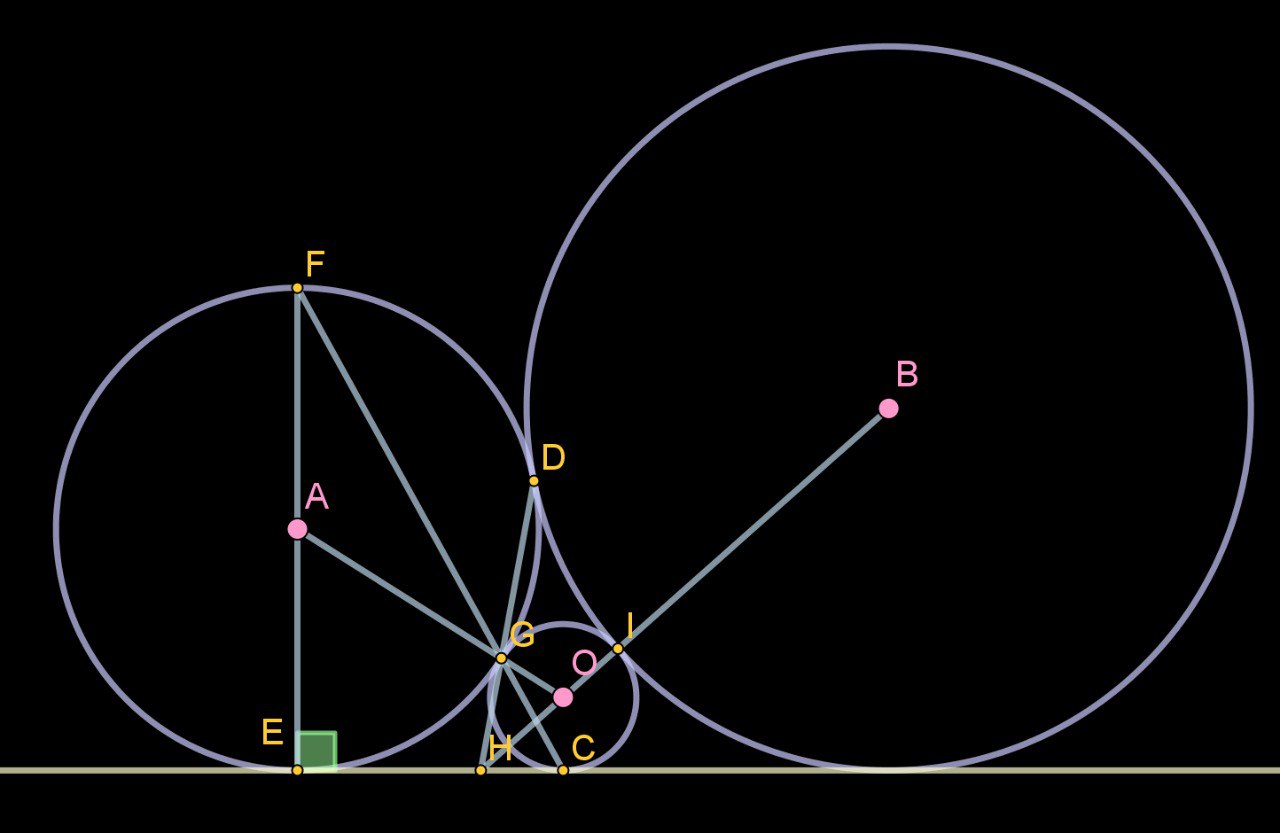
0) Придумайте короткий способ построить точку пересечения искомой красной окружности с общей касательной. Центры кругов (A и B) считаем известными, общая касательная тоже уже есть.

1) Пусть эта точка (С) уже построена. Докажите, что точку касания (G) с голубой окружностью можно построить, просто найдя пересечение отрезка CF с этой окружностью, где F - точка окружности, симметричная точке касания E.

Соответственно, можно аналогично построить и точку касания со второй окружностью, а затем найти искомый центр в пересечении AG и BI. Но есть и другой вариант:

2) Докажите, что центр O получается в пересечении AG с прямой BH - где H точка пересечения DG с общей касательной.

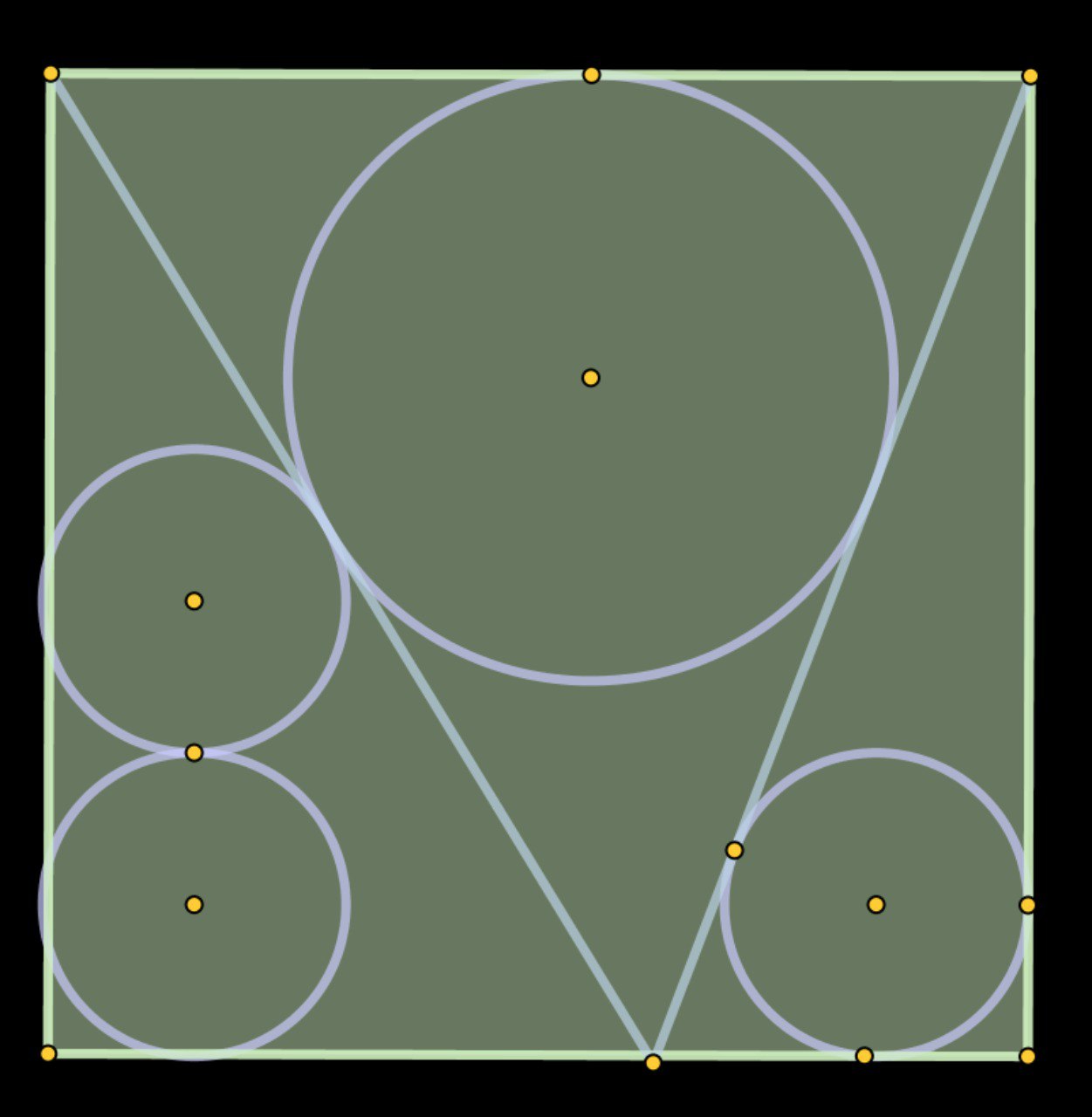
Amirul Faiz (если не ошибаюсь, из Малайзии) несколько дней назад опубликовал такую вот задачу:

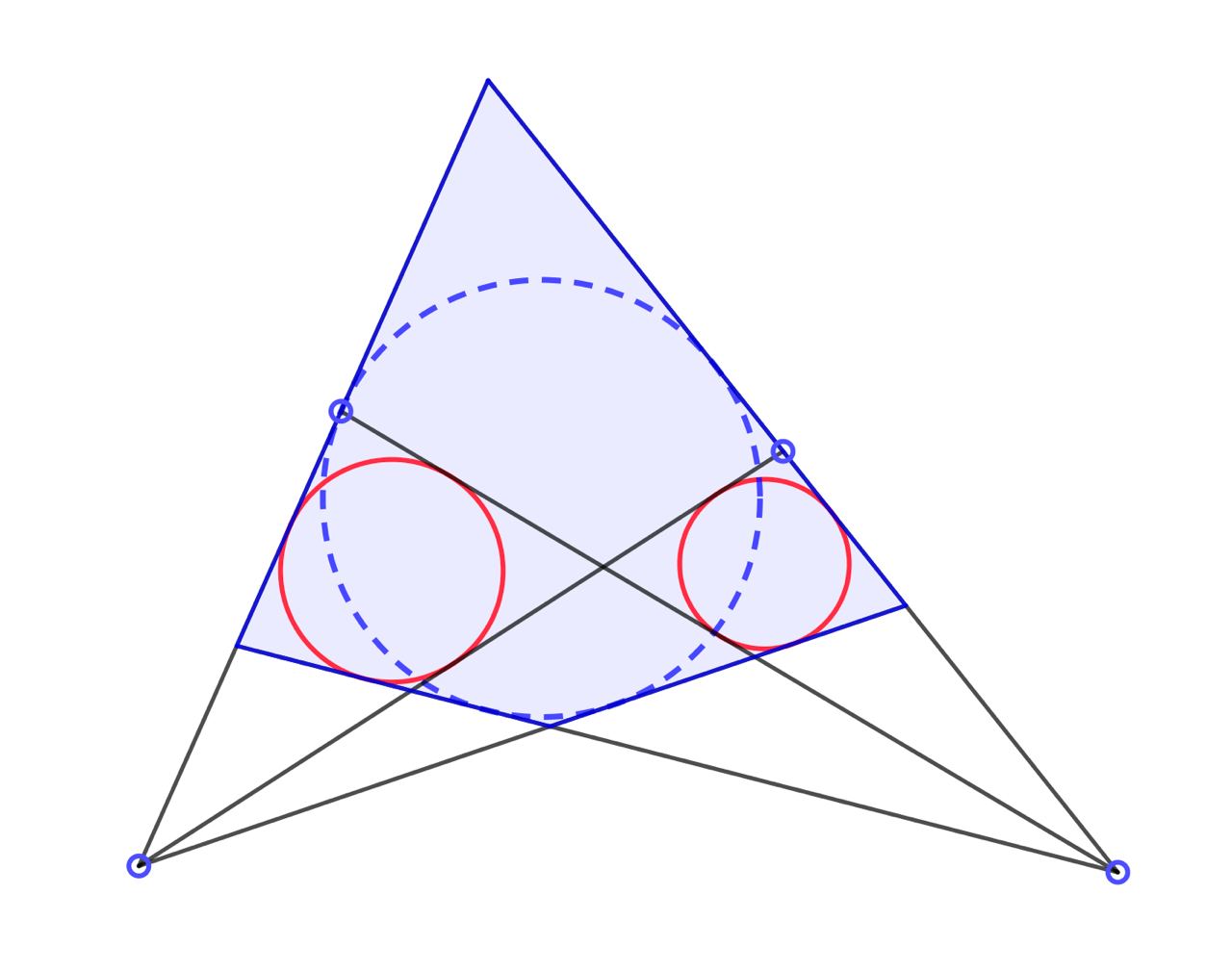
В квадрат вписаны 4 окружности, как показано на рисунке (в левом треугольнике две, в правом одна, в верхнем еще одна). Общая точка треугольников лежит на стороне квадрата. Радиусы трех маленьких окружностей равны 1. Найдите радиус большой окружности.

---
Конечно же, ее решили — предложено несколько решений с тригонометрическими вычислениями и парочка с алгебраическими. Но чисто геометрического решения предложено не было. Дерзайте!

Может показаться, что большая окружность касается одной из маленьких. Это не так. По крайней мере, частью условия это свойство не является.

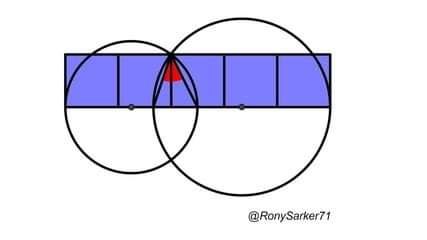
#задача

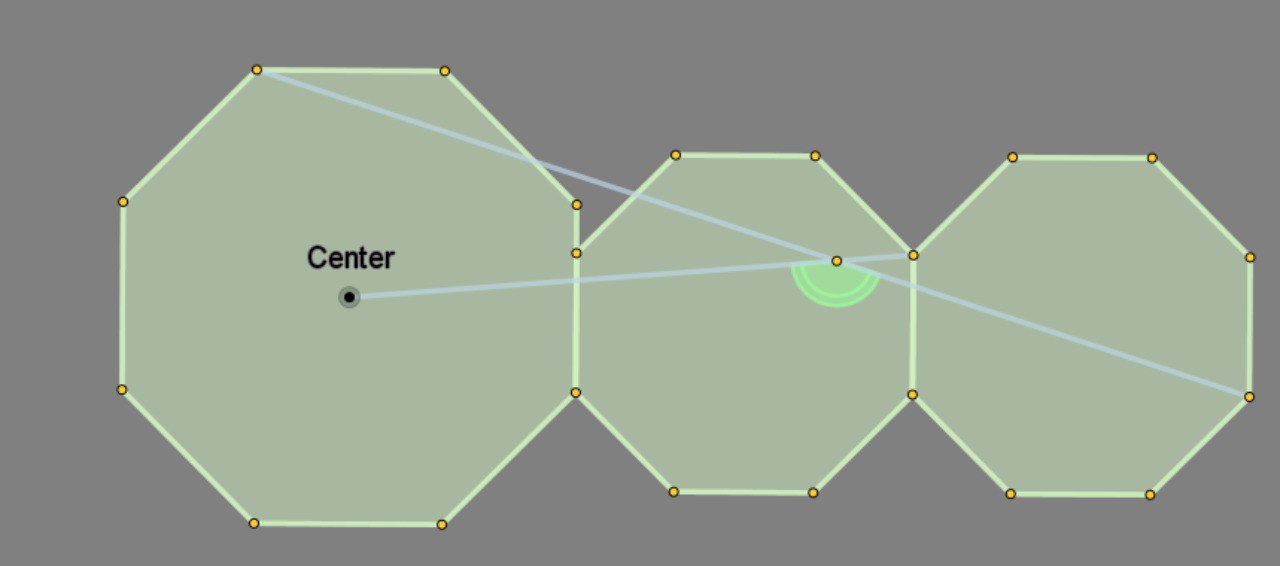
Усложнение задачи RonySarker. Интересно, как с нею справятся многочисленные любители тангенса суммы...

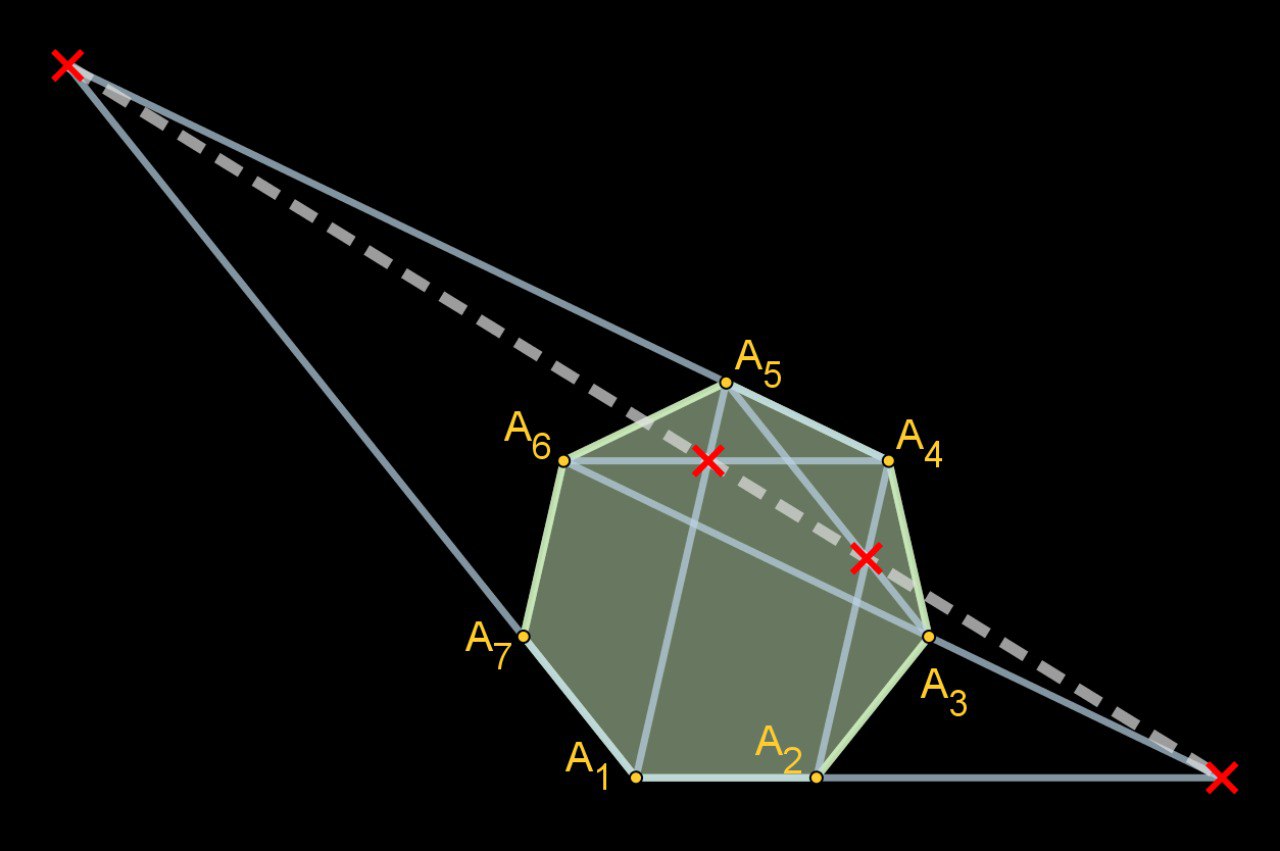
Алгебра с геометрией...
Дан правильный семиугольник. Докажите, что четыре точки, обозначенные крестиками, коллинеарны (лежат на пунктирной прямой)

и еще один ролик про сангаку — в т.ч. предлагается решить задачу про «хвост павлина»

https://youtu.be/ZDJbJzq2SR4

внутри геометрического чатика Сергей Беляев показыват еще фото оригинальной таблички с задачкой «павлиний хвост» и рассказывает разное про сангаку

https://youtu.be/4hW9vo8ycOs

коллега Мухин рассказывает про задачу Фаньяно и т.п.

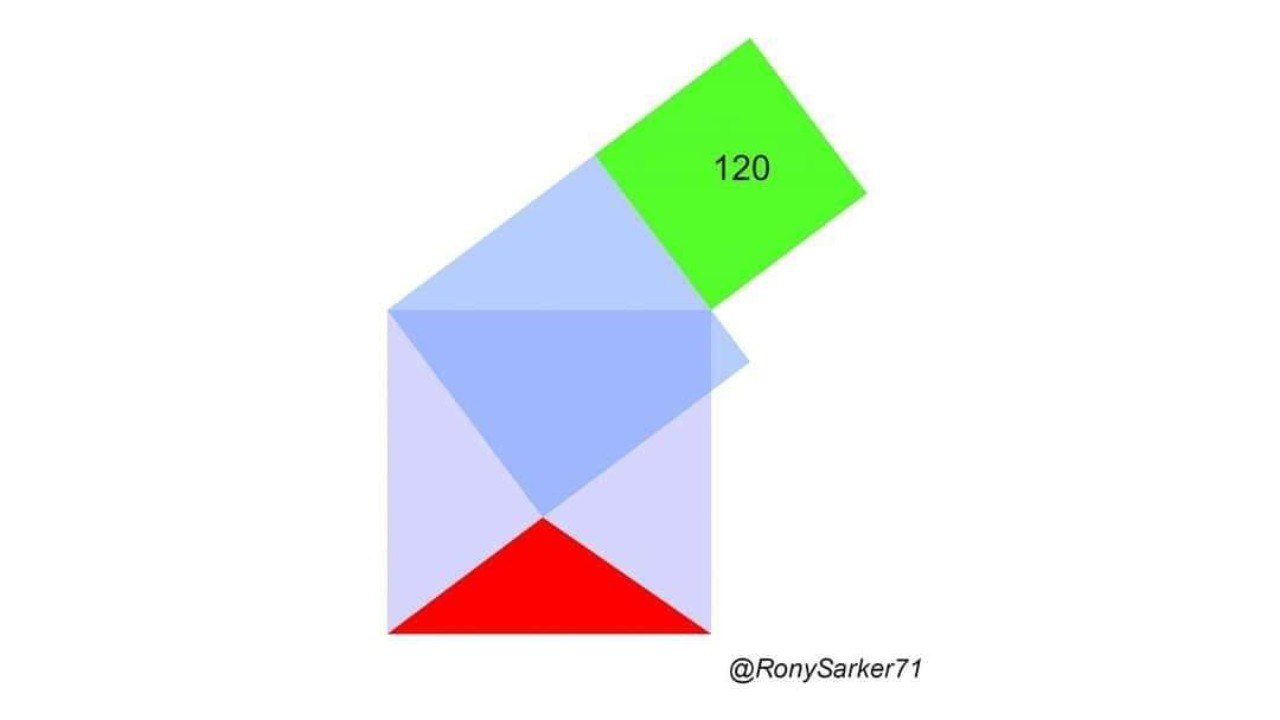
На рисунке - три квадрата и один треугольник. Чему равна площадь (красного) треугольника?

развитие сюжета про самые короткие пути есть еще в статье В.Ю.Протасова «Точка Торричелли и сети Штейнера» (№№10-12 журнала «Квантик» за 2021 год)

#задача по мотивам разного недавнего (via А.Щетников):

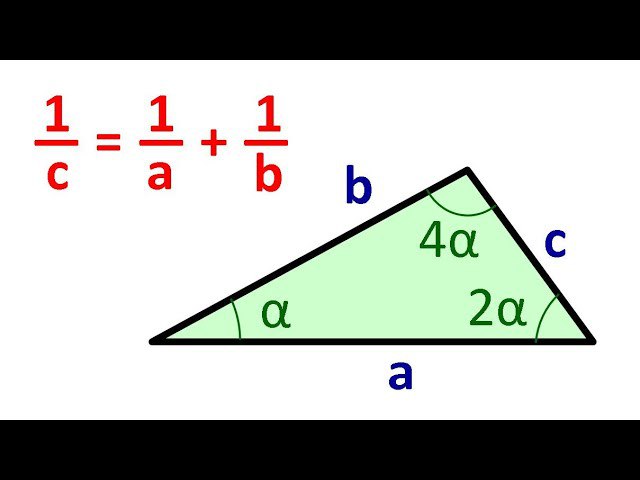
доказать, что для сторон треугольника, углы которого относятся как 1:2:4, выполнено соотношение 1/a+1/b=1/c

(можно что-то посчитать, а можно найти и более геометрическое решение… видимо даже есть разные)

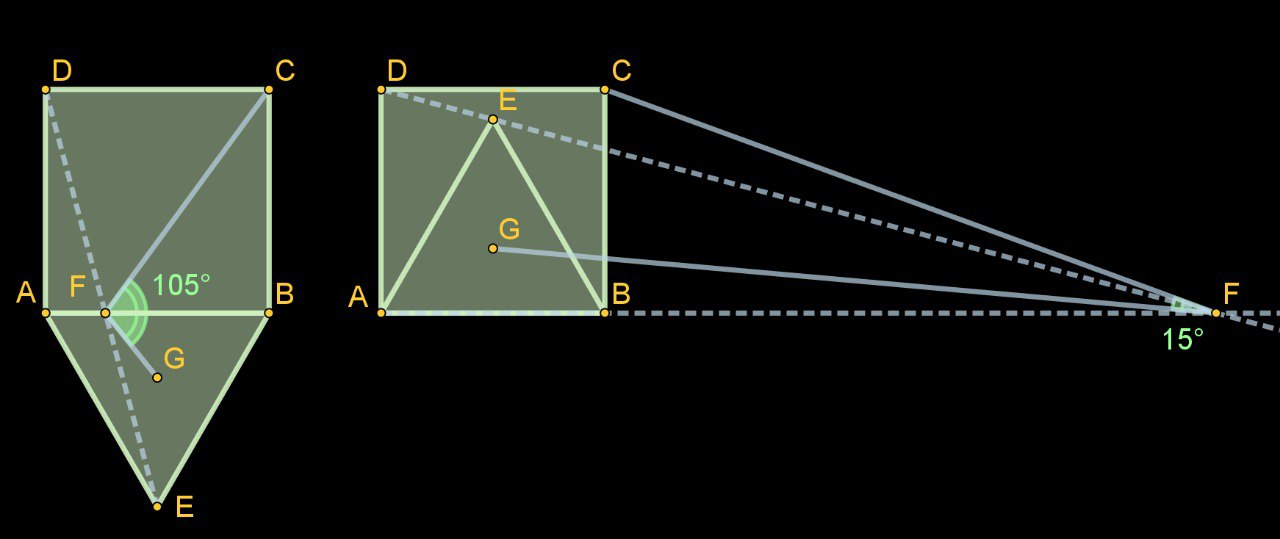
Очередной вызов для true-геометров
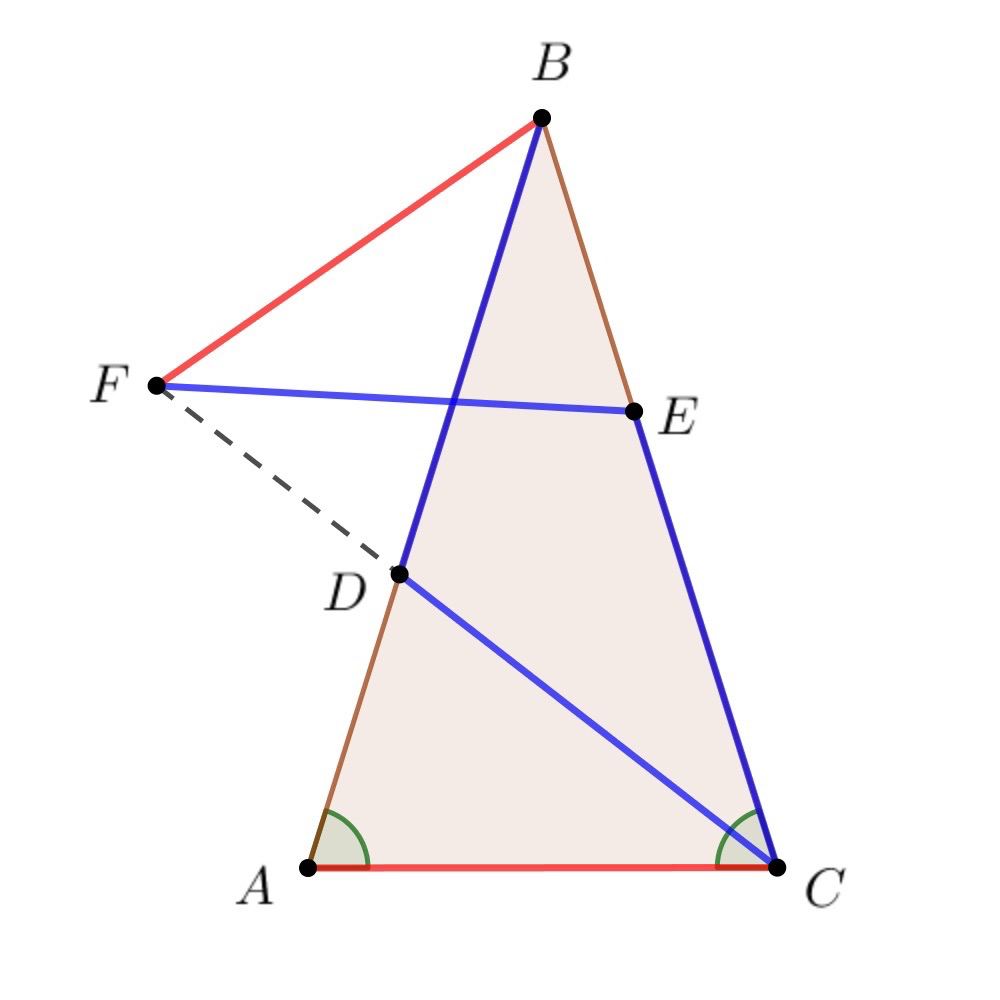
На левом чертеже изображена задача Binh Luc, недавно опубликованная им в одной из англоязычных "геометрических" групп. В ней предлагалось найти угол CFG (F - точка пересечения стороны AB и отрезка, соединяющего третью вершину равностороннего треугольника с одной из вершин квадрата, - оба правильных многоугольника имеют AB своей стороной; G - центр этого треугольника, C - четвертая вершина квадрата). Эта задача, безусловно, была решена алгебраически (там несложные вычисления, что в координатах, что тригонометрические...). Но настоящие геометры, как известно, так не поступают.
Предлагаю доказать, что этот угол равен 105 градусам, а заодно и потренироваться на парной задаче - доказать в ней, что аналогичный угол равен 15 градусам.
Маленькая подсказка: оба решения исходят из того, что мы легко можем увидеть на рисунке углы 45 и 30.

давайте попробуем восстановить традицию не только задач, но и решений в этом канале?

для разминки: два решения задачи выше можно узнать из ролика https://youtu.be/1N-doa1KZeE