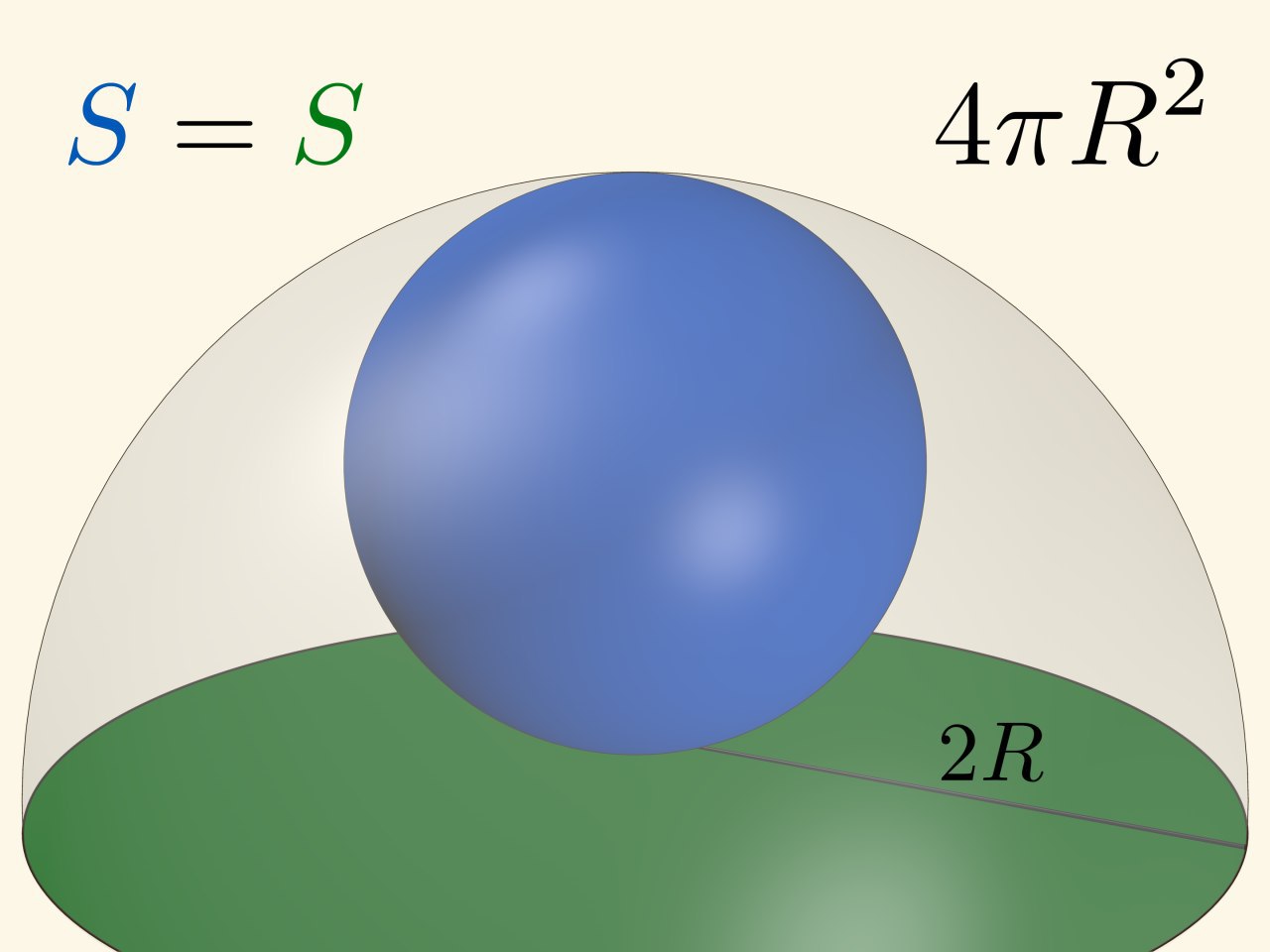
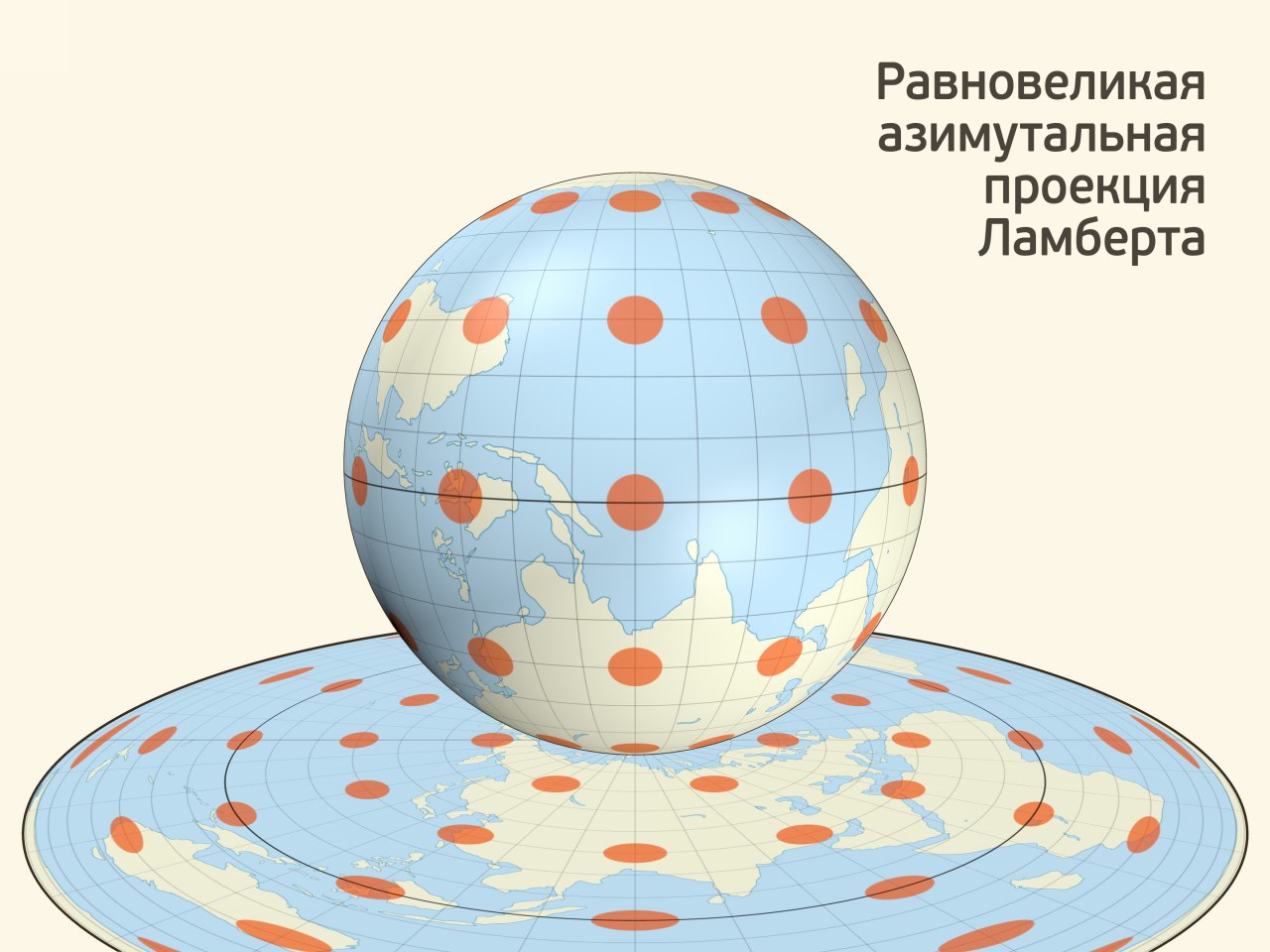
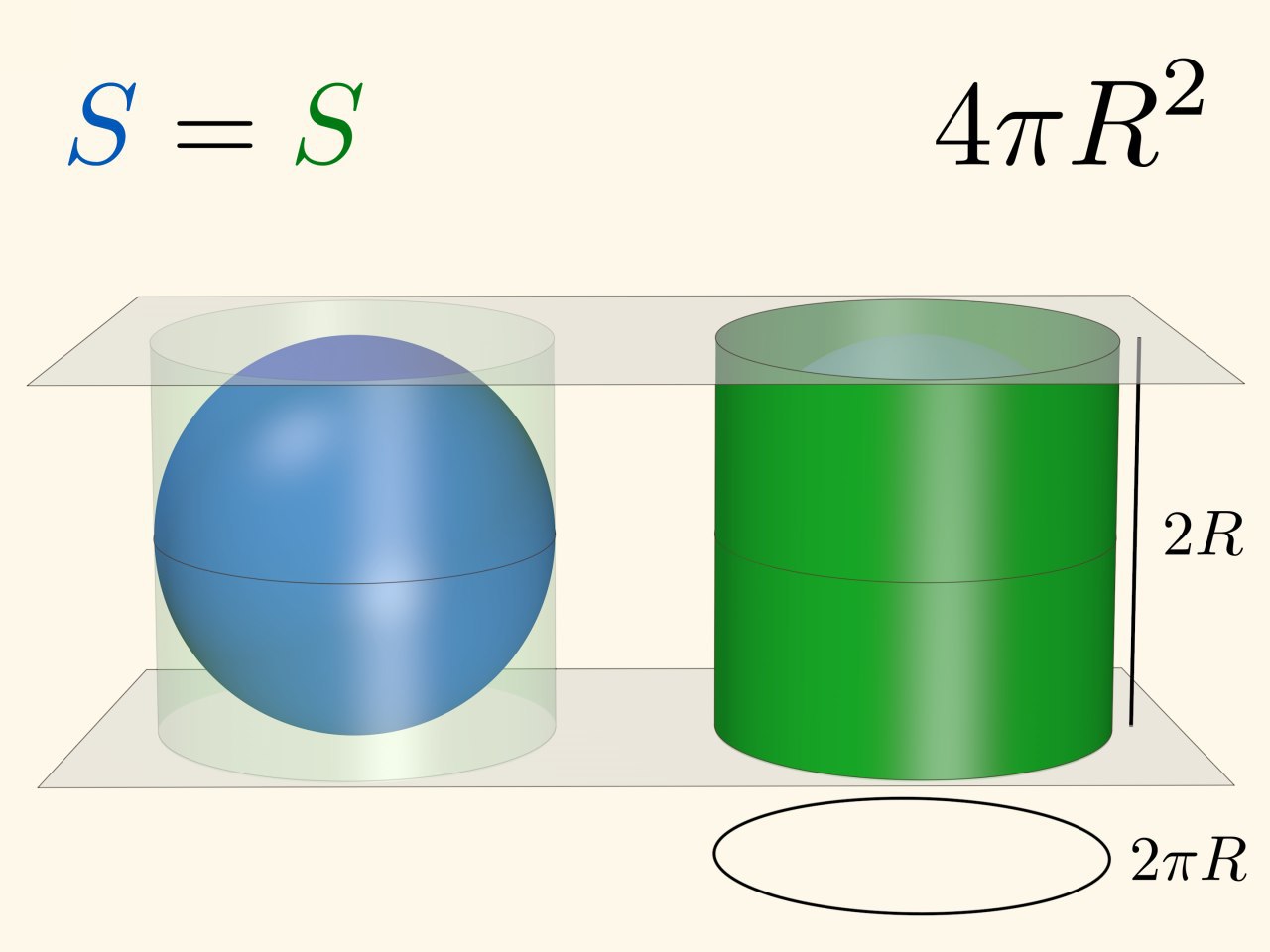
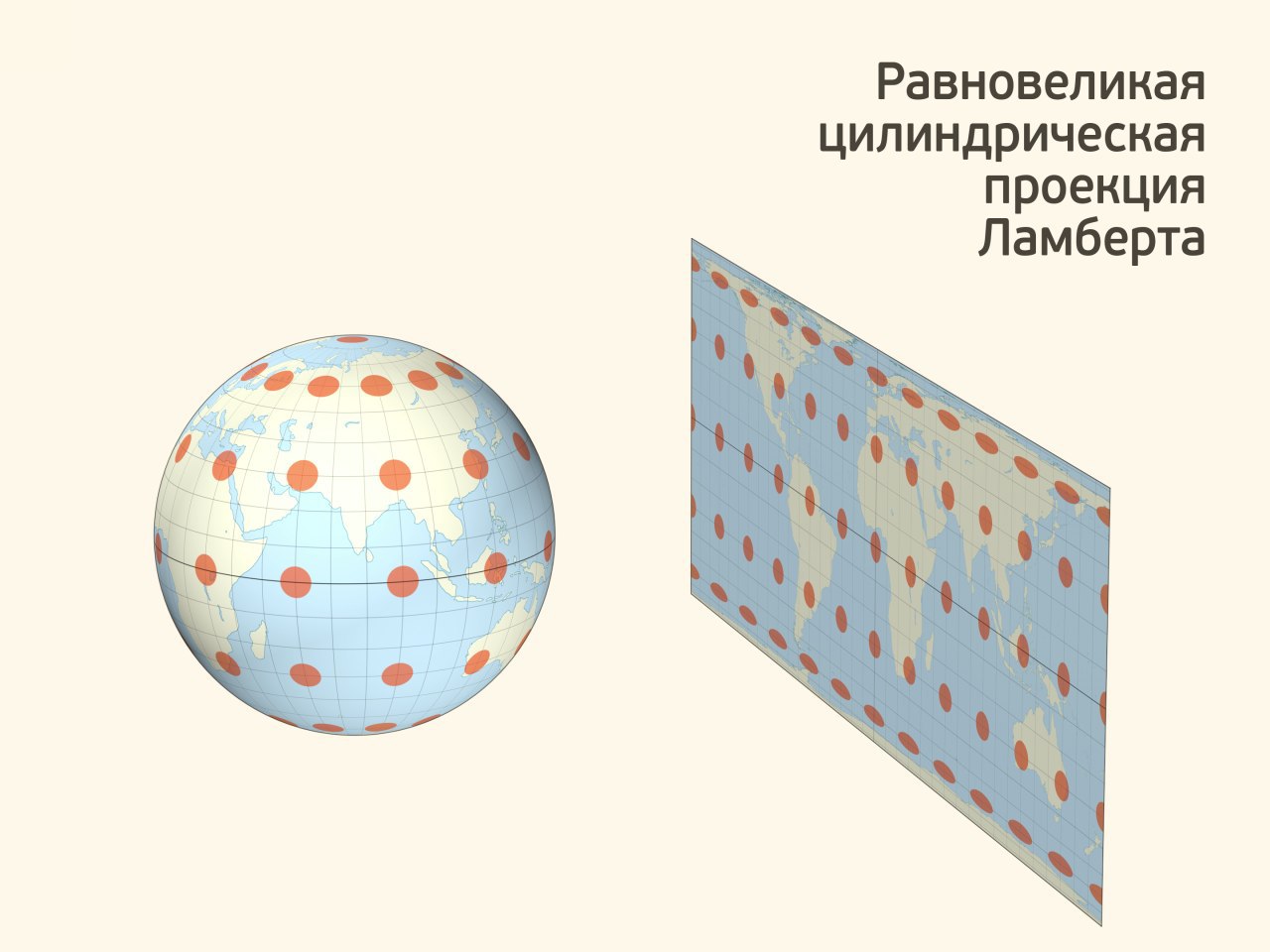
Утверждение про площадь сферической шапочки и площадь круга «того же радиуса» тоже довольно известно. Оно позволяет легко запомнить формулу площади поверхности сферы, позволяет строить равновеликую картографическую проекцию, уже азимутальную.
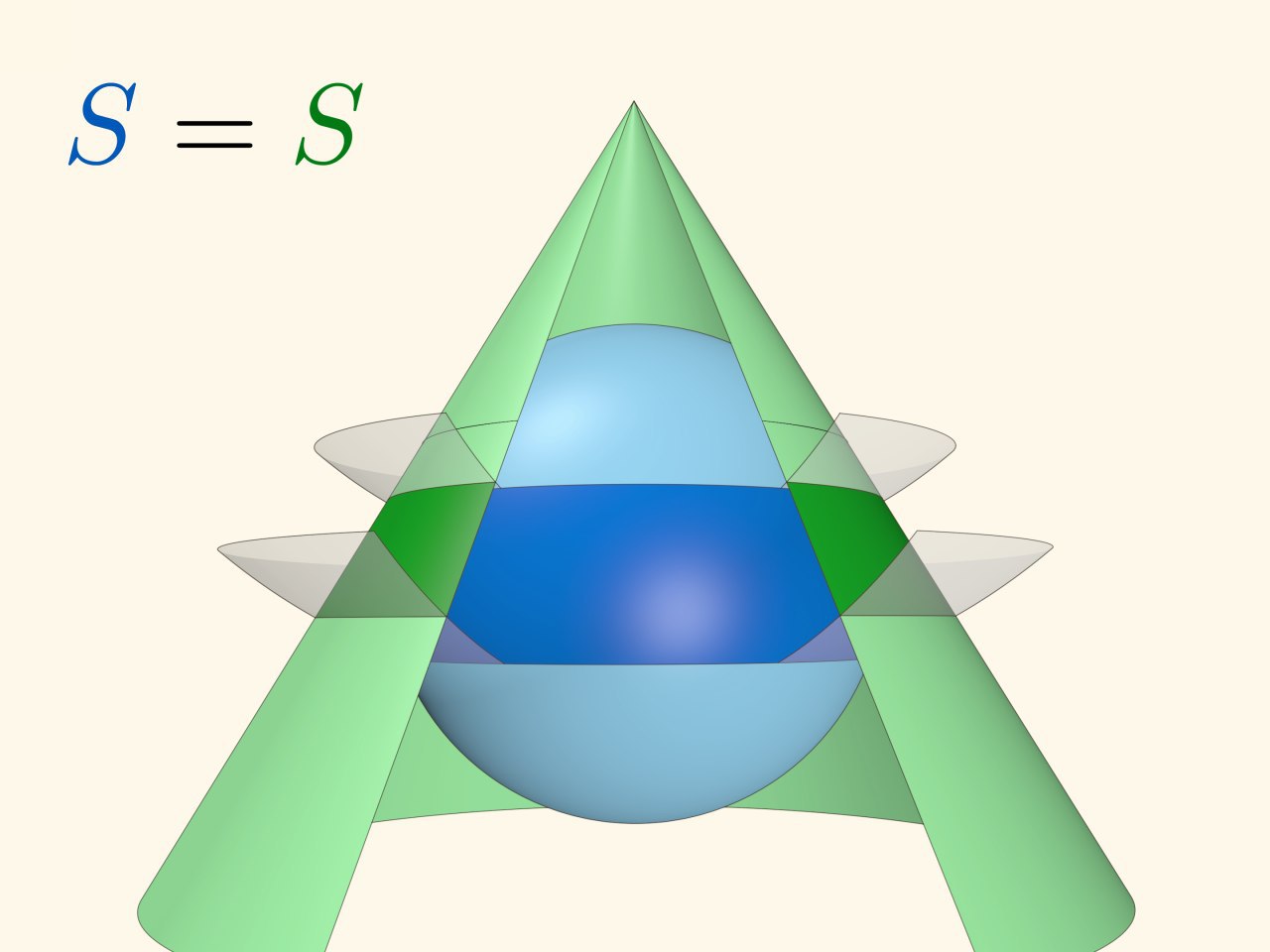
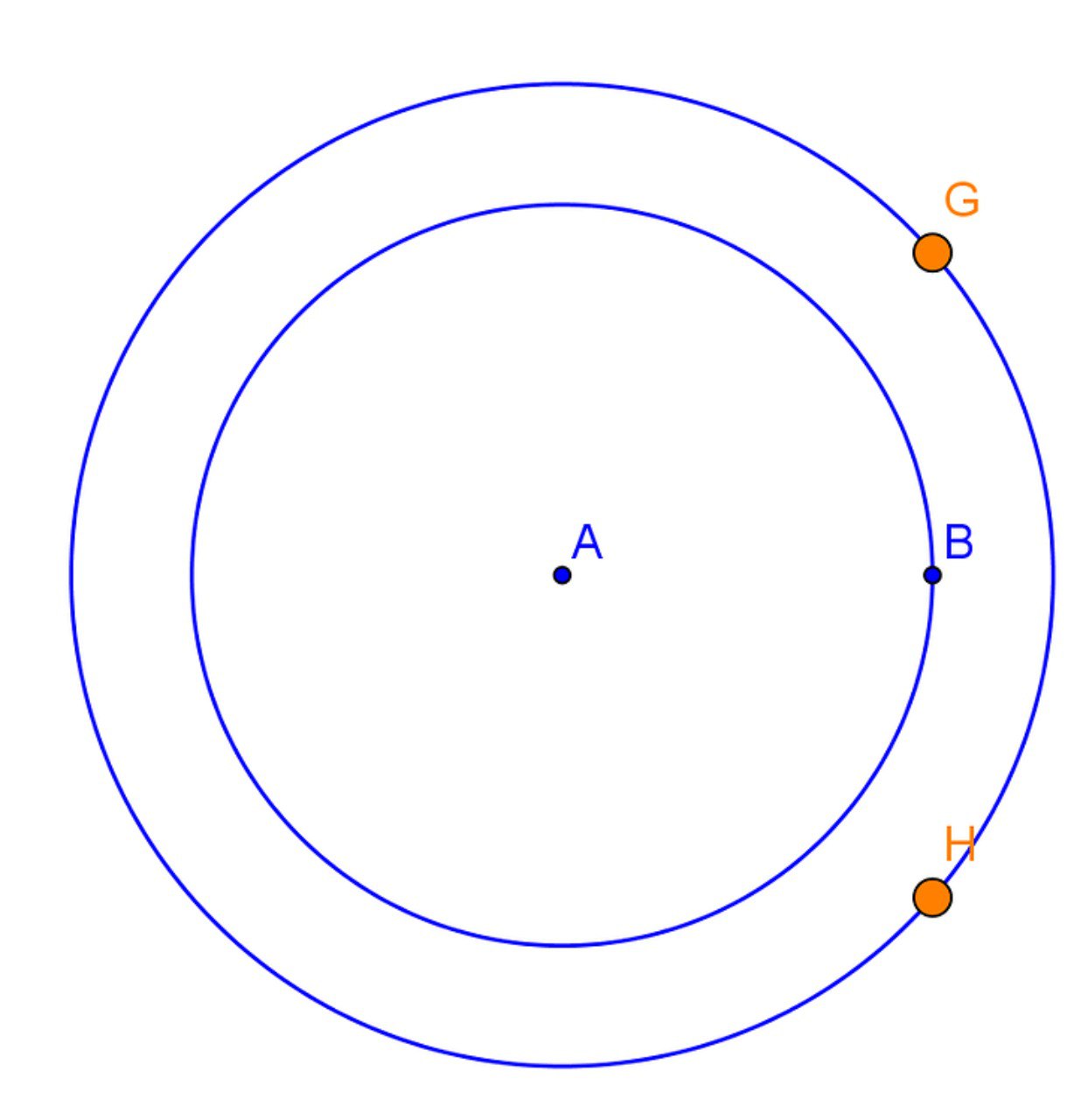
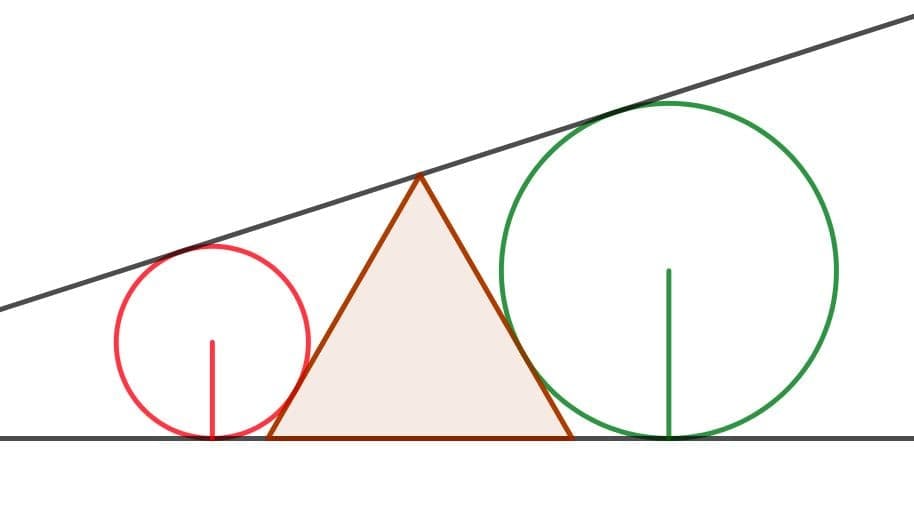
Удивительно, что связывающая эти два случая конструкция – сравнение площадей колец на сфере и на конусе, заключённых между концентрическими сферами с центрами в вершине конуса – малоизвестна. Ещё более удивительно, что вроде как первая публикация (а может кто-то знает более раннюю ссылку?) была лишь в 2006 году (в одном из старейших научно-популярных журналов по математике и математическому образованию – «The Mathematical Gazette»).
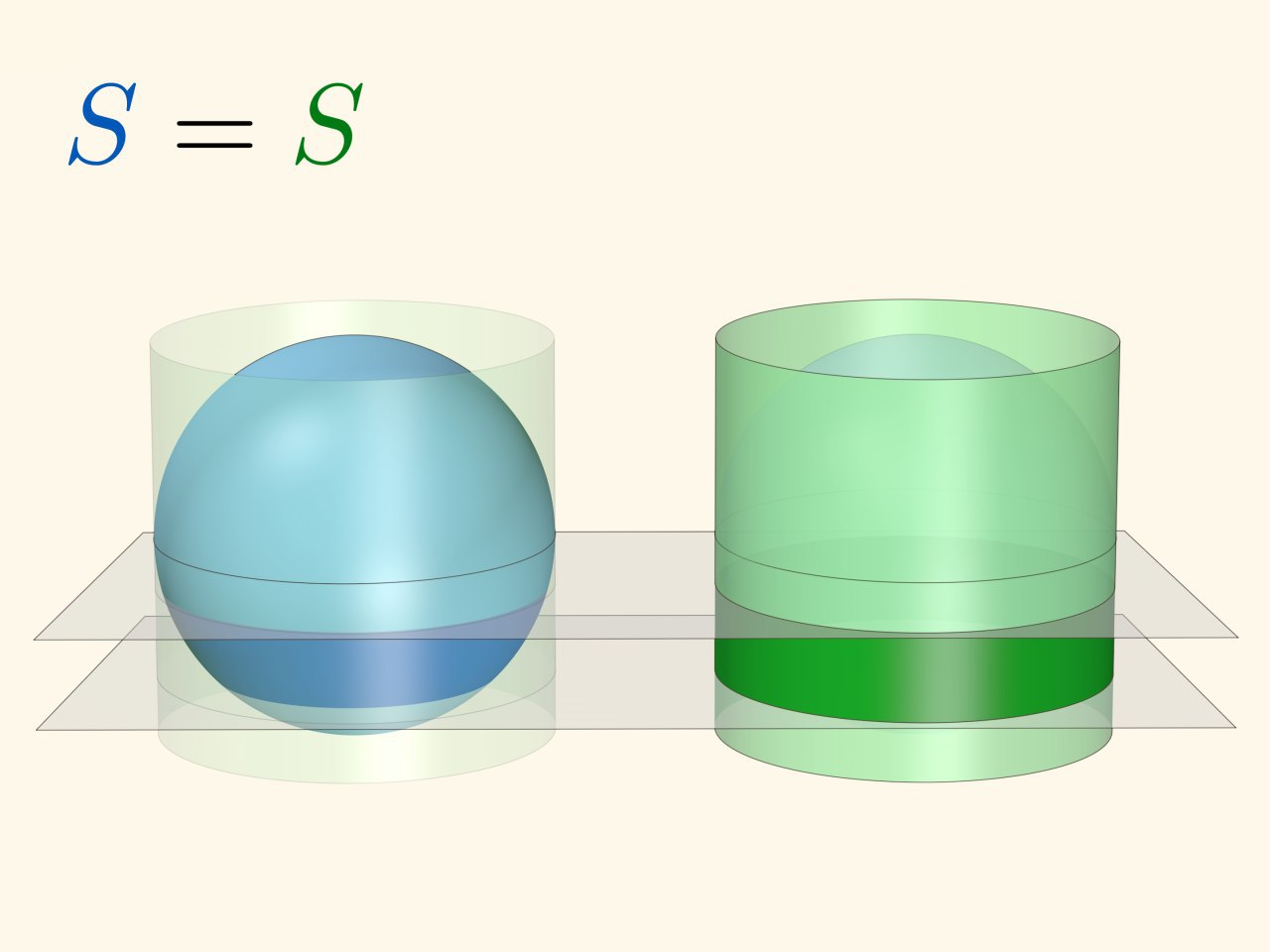
Сегодняшняя премьера Математических этюдов – фильм «Площадь на сфере: сферы, шапочки, кольца», повествующий о том, как посчитать площадь сферического кольца и, соответственно, всей сферы, сравнивая её с площадями круга, кольца на цилиндре и конусе.
А появился фильм благодаря статье Арсения Акопяна (автора суперпопулярной необычной книги «Геометрия в картинках») в 9 номере этого года журнала Квант. Спасибо Арсению – конический случай очень красиво объединяет общеизвестные.