Всем привет! На канале Маткульт-привет Алексея Савватеева вышло видео с Юрием Маркеловым про задачу 255. Юрий обещает целый курс по интересным сюжетам олимпиадной геометрии! Не знаю как вы, а я буду следить за тем, что там и как получается. Чем больше хороших источников знаний по геометрии, тем лучше! Думаю, Юра будет очень рад конструктивной критике, лайкам и подписчикам (у Юры, кстати, есть свой канал — ищите ссылку в описании видео на Youtube).

https://m.youtube.com/watch?v=YOhJB2oYSF4

Участвуй в конкурсе домашних  научных экспериментов и выиграй планшет Samsung Galaxy Tab A7!😋

С 24 мая по 1 июля компания 3M проводит конкурс научных экспериментов для школьников от 6 до 17 лет.

👉Всё проще простого:

1. Смотри крутые эксперименты из химии, физики, биологии от экспертов на сайте «Наука дома»
2. Повтори на камеру один или сразу несколько из этих экспериментов самостоятельно или с родителями — главное, соблюдай меры безопасности.
3. Запости видео у себя в соцсети (Instagram, TikTok или ВКонтакте) с хэштегом #3Mнаукадома с 24 мая по 1 июля.
4. Трёх экспериментаторов-победителей объявят 15 июля, они выиграют планшеты Samsung Galaxy Tab A7!🏆

Присоединяйся, ведь наука — совсем не скучная штука!🤘
Читай подробнее о конкурсе и смотри видео на сайте «Наука дома»

#реклама

Разговорились мы тут в геометрическом чатике о том как догадываться до решения геометрической задачи. Challenge accepted!  Последнее событие в нашем геометрическом мире это конечно лекция Юры Маркелова (см. видео выше). Задачи EASY и MEDIUM попробуйте решить сами. А вот задачка HARD - интересная. Давайте вместе попробуем догадаться как её решать. Внимание: спойлер! Не смотрите это видео если хотите решить задачу самостоятельно. У этой задачи (как у всякой красивой задачи) наверняка есть и другие способы решения. Я показал первый, которые мне пришёл в голову.
https://www.loom.com/share/7c41fc29db8649d6a78800b48a456098

https://youtu.be/fEinV81foBA

«…одна и та же задача может иметь “вложенные“ в нее интересные частные случаи, и в то же время может оказаться “вложенной” в более общую теорему. О примерах таких “математических матрёшек”  рассказывает Павел Александрович Кожевников…»

дело доходит, кстати, и от элементарной планиметрии до обсуждавшихся чуть выше кубических кривых, и еще до разного

В уме докажете, что это 3-4-5 треугольник?
Источник

Сегодня музей математики в Нью-Йорке проводит онлайн-встречу с Катрионой Эгг (Ширер). Ее задачи тут иногда появлялись. Если зарегистрироваться, можно поучаствовать, это в 23:00 МСК.

Это встреча в рамках цикла «Разговоры с математиком» — там есть и другие.
Подробности: https://momath.org/meet-a-mathematician/

Пара доказательств теоремы об окружности 9 точек: https://youtu.be/BOXXct5wJXI

#видео

Олимпиада для всех желающих

Во вторник, 6 июля, пройдет онлайн-олимпиада по математике. Олимпиада рассчитана на школьников, студентов, учителей и всех интересующихся математикой.

Подробности и регистрация: https://vertical.sch-int.ru/leto-2021-6jul/

А вот и вторая серия лайфхаков Геогебры, спасибо всем тем, кто прислал свои. 16 минут видео, а там: вспомогательные чертежи в стереометрии, работа с графиками, полезные команды в планиметрии, интеграция GGB с продуктами Microsoft Office.

https://youtu.be/8dGtGOPNT5o

Приходите обсудить в чат «Геометрия на подвижных чертежах» https://t.me/joinchat/Eg7psxQ1MLIrk1bKwOjS8A

Мы когда-то тоже так развлекались

А вот тут целая подборка таких задач

#реклама

Школьное обучение на иностранном языке — возможно!

International School of Kazan открывает набор в 5–10 классы.

Вашего ребенка будут обучать только квалифицированные специалисты из Европы и США. Каждый педагог с интересом преподносит информацию и готовит к ЕГЭ, повышая успеваемость ученика.

В Международной школе Казани удачно сочетается всестороннее развитие, прогрессивное образование и внимание к детям. После окончания школы учащийся получает российский аттестат и диплом международного бакалавриата.

Переходите на сайт, чтобы открыть для себя новый мир в учебе!

​​Проблема Хееша. Если есть многоугольник, и мы хотим определить — можно ли им выложить всю плоскость?

Напрашивается алгоритм — выложим его копиями первый слой вокруг себя, потом второй, третий и дальше. Если достаточно много слоёв выложено — наверное, им можно выложить плоскость.

Это открытая проблема. Никто не знает, существует ли такое n, что если в n слоёв выложить можно — то это гарантия, что и дальше вся плоскость выложится.

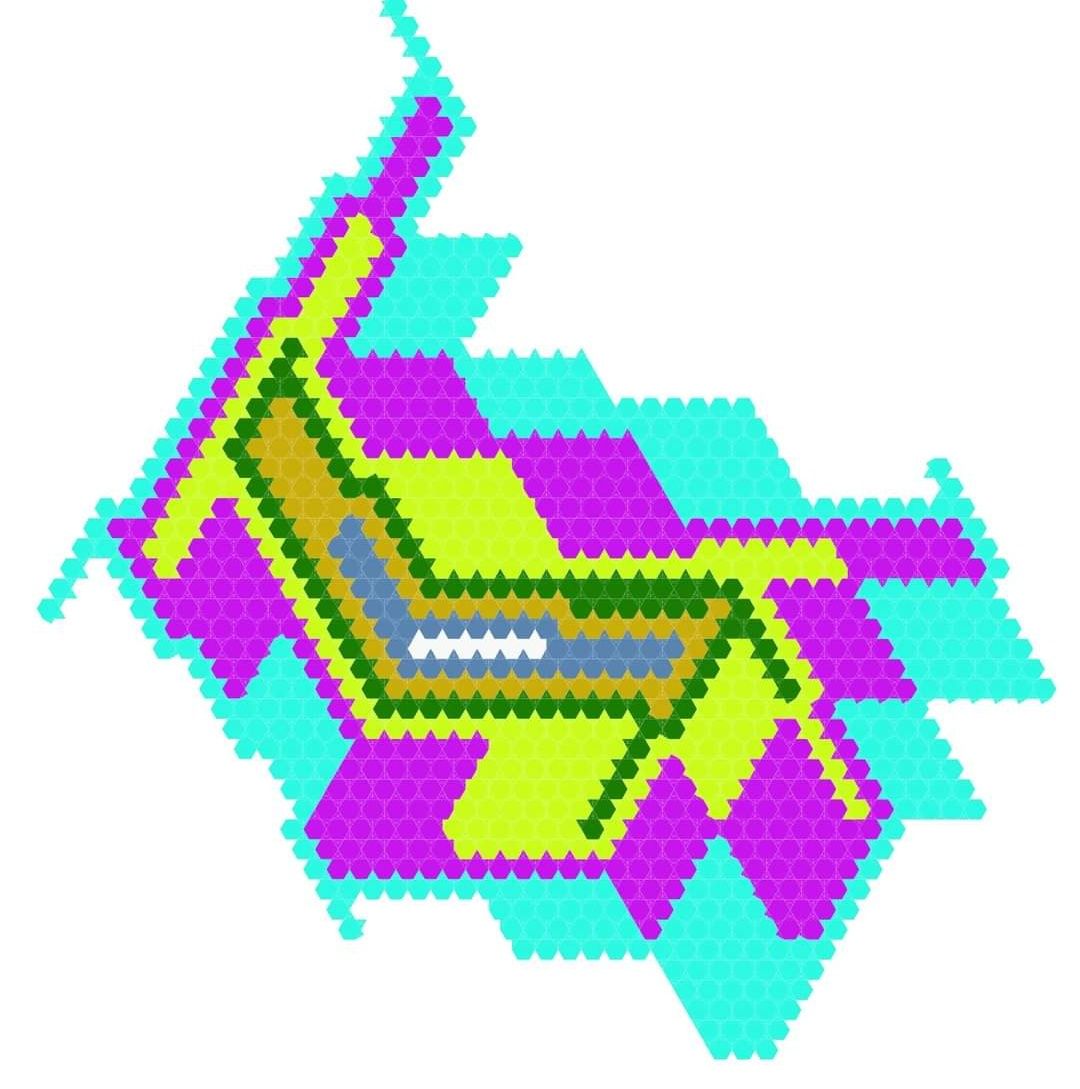
Журнал Mathematical Intelligencer опубликовал статью Bojan Basic с новым рекордом. Приведён пример многоугольника, которым можно выложить 6 слоёв вокруг себя, но всю плоскость — нельзя.

На сегодняшний день все известные многоугольники, которыми можно в 7 слоёв выложить вокруг себя — можно и бесконечно много выложить вокруг себя. Но верно ли это в целом? Никто не знает. Нет никакой конечной оценки. Существует ли многоугольник, который можно в миллион слоёв выложить вокруг себя — но замостить им плоскость невозможно? Открытая проблема.

На картинке сам многоугольник с числом Хееша 6.

Источник: Bašić, B. A Figure with Heesch Number 6: Pushing a Two-Decade-Old Boundary. Math Intelligencer (2021). https://rdcu.be/cpgpy

Популярное объяснение проблемы Хееша по-русски, предыдущие многоугольники-рекорды. Хайдар Нурлигареев
«Квантик» №10, 2019 https://elementy.ru/nauchno-populyarnaya_biblioteka/435227/Plitki_i_chisla_Kheesha

Видео о проблеме Хееша (eng): https://youtu.be/6aFcgATW9Mw

Спасибо Сергею Маркелову за публикацию на фейсбуке: https://www.facebook.com/groups/mathpuz/permalink/1963290000513499/

Это он и 6 слоев вокруг

задачи проходившей вчера и сегодня международной математической олимпиады

Всем привет! Разбираем задачу номер 3 с Международной математической олимпиады этого года!https://youtu.be/gh0ZJAV_ZCQ